
本記事では、(株)データミックスの「気象データアナリスト養成講座」を受けた感想や、講義メモをまとめます。
今回は、2023年3月18日に受けた、ベーシックステップ1日目の内容です。
回帰分析:線形回帰

講義8日目の内容は、回帰分析の「線形回帰」でした。
線形回帰は、売り上げや動画の再生時間など連続量を扱う分析です。
講義9日目には、回帰分析の「ロジスティクス回帰」を扱う予定です。
ロジスティクス回帰は、広告のクリックの有無などカテゴリを扱う分析です。
モデルとは

モデリングすることで、以下のことができます。
- yとxの関係性を把握
- xからyを予測
関係性を把握するのは、統計的なアプローチになります。
予測するのは、機械学習的なアプローチになります。
回帰と分類
モデリングは、「回帰」と「分類」に分けることができます。
- 回帰:連続値を予測する
- 分類:カテゴリを予測する(0か1か)
予測精度を重視したいときは、機械学習的にアプローチしていきます。(ML的アプローチ)
ML的アプローチはモデルが複雑になりやすく、ブラックボックス化しがちです。
なので「モデル内で何が起きてるか」を人間が把握するのは難しくなります。
ただし、ML的アプローチにおいても解釈は大切になるので、「どの特徴量が効いたか」などの説明性も求められるそうです。
統計的なアプローチは、比較的シンプルなモデルになります。
人間が理解しやすいというメリットがある一方、複雑な事象を捉えにくく、予測精度が落ちてしまうというデメリットもあるようです。
多変量モデルの考え方
まず、変数が2つのときのモデルは、以下のようになります。
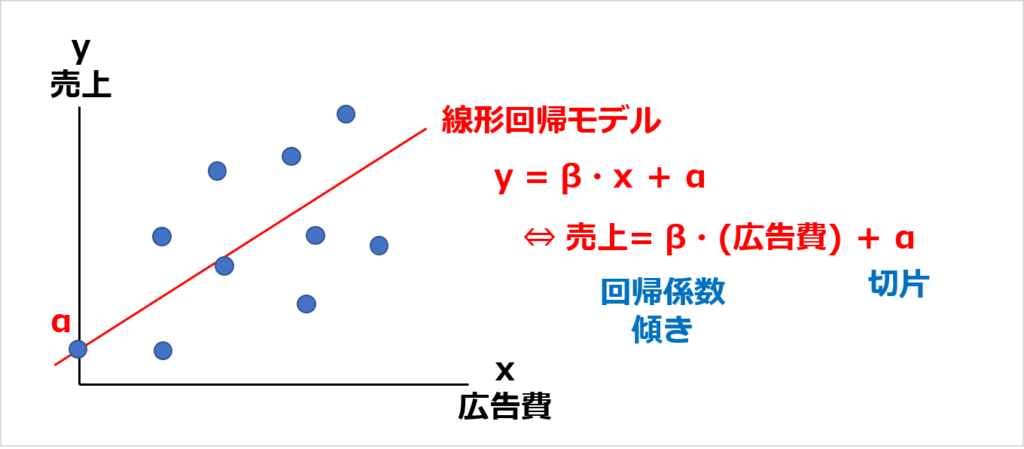
2次元なので、線形回帰モデルは直線になります。
次に、変数が3つのときのモデルは、以下のようになります。
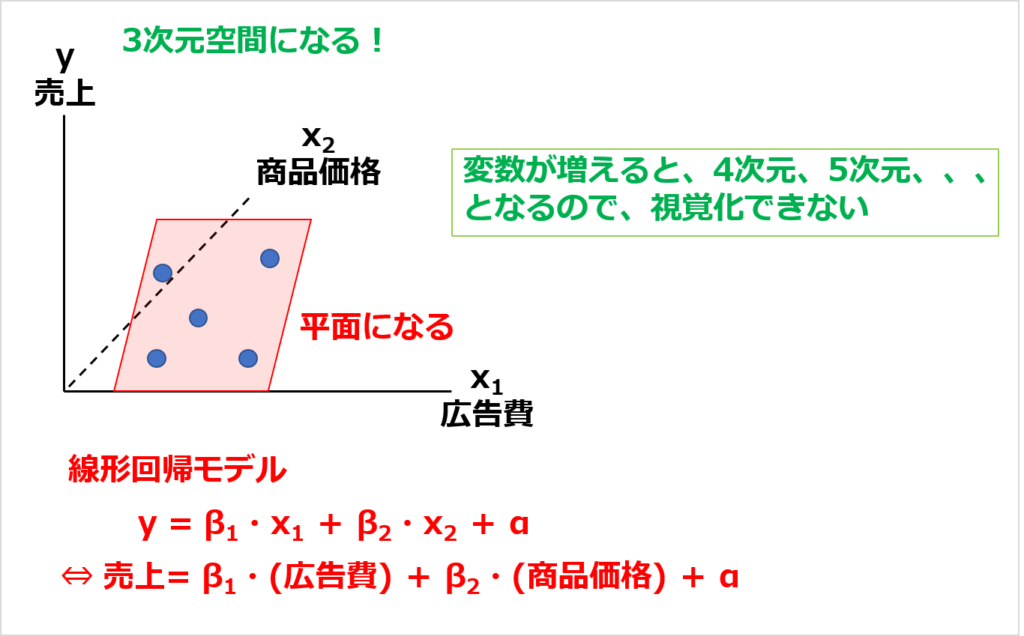
3次元なので、線形回帰モデルは平面になります。
変数を複数にしていく(=多次元にしていく)と、より精度高く予測できるようになります。
多次元の空間に散らばっているデータを線形的な関係でとらえていくのが、モデリングでやることです。
線形的な関係をとらえるために、直線や平面を決めるパラメータ(切片や回帰係数)を推定していきます。
線形回帰の前提条件
線形回帰は、4つの前提条件が成立することを仮定しています。
前提条件
- 線形性:「目的変数」と「説明変数」は線形の関係である
- 等分散性:データの残差は等分散である
- 正規性:誤差は正規分布に従う
- 独立性:観測データはお互いに影響しない
- 線形性
線形回帰では、「目的変数」と「説明変数」が線形の関係であることを前提としています。
線形の関係とは、直線でモデル化できるデータの分布です。
線形ではない関係を考えてみると、例えば「電気代」と「気温」の関係が挙げられます。
気温が高くなると電気代も上がりますが、気温が低くなればなるほど電気代が下がるわけではありません。
「電気代」と「気温」は、非線形の関係として考えます。
- 等分散性
線形回帰では、「残差」が等分散であることを前提としています。
すなわち、「残差」は予測した回帰直線に沿って同じように散らばっていることを想定しています。
- 正規性
線形回帰では、「誤差」は正規分布していることを前提としています。
回帰直線に近いところにデータが集まっていて、回帰直線から離れれば離れるほどデータ数は少なくなると考えられます。
そのため「誤差」の分布を考えると、正規分布になります。
- 独立性
線形回帰では、ひとつひとつの観測されたデータは、お互いに影響を及ぼしていないことを前提としています。
例えば、ある日の売上データが10万円、別の日の売上データが13万円だったとき、「10万円」と「13万円」は独立したデータだと考えます。
これが「体重」のように時系列データになると、ある日の体重は前日の体重の影響を受けてしまうので、独立性があるとはいえません。
R言語で単回帰分析

ここからは、Rを使って単回帰分析をやってみます。
実際の講義では、ユニセフのデータを使って進められました。
今回は、Rのデータセットにある「cars」のデータを使って分析します。
データのセットアップ
はじめに「cars」のデータを読み込み、どんなデータになっているのか見ていきます。
data(cars) ### データセットを読み込む head(cars) ### 見出しを確認 View(cars) ### 表が出力される cars %>% glimpse ### 横方向にデータの一覧を見れる
「View(cars) 」の結果は以下の通りです。
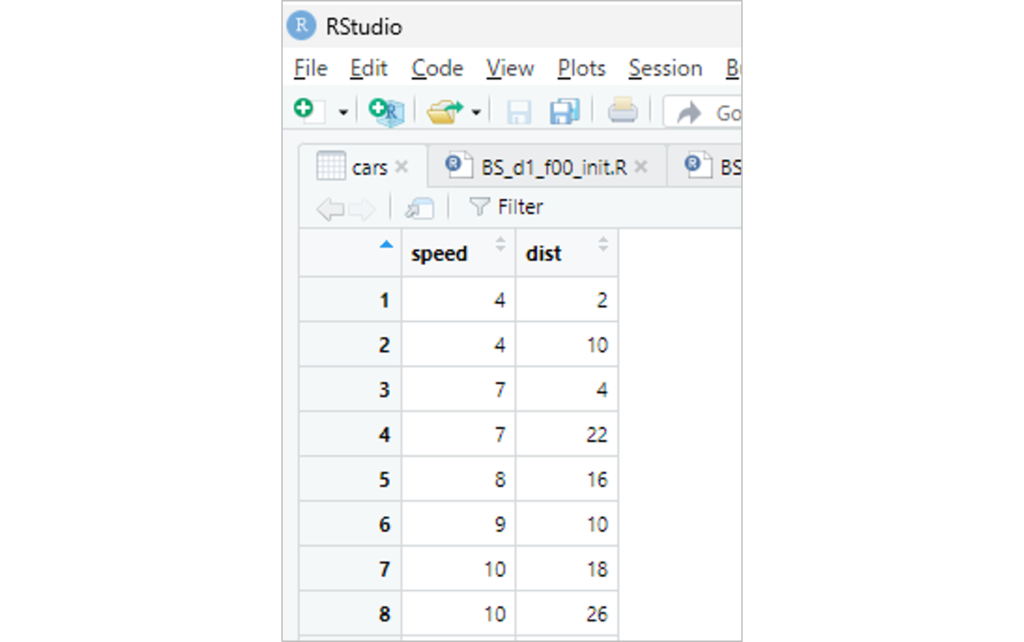
「cars」のデータは、「speed:速度」と「dist:距離」のデータが50列あります。
- 散布図
続いて、散布図を描いて「speed:速度」と「dist:距離」の関係を見ていきます。
plot(cars, main = "cars") ### 散布図
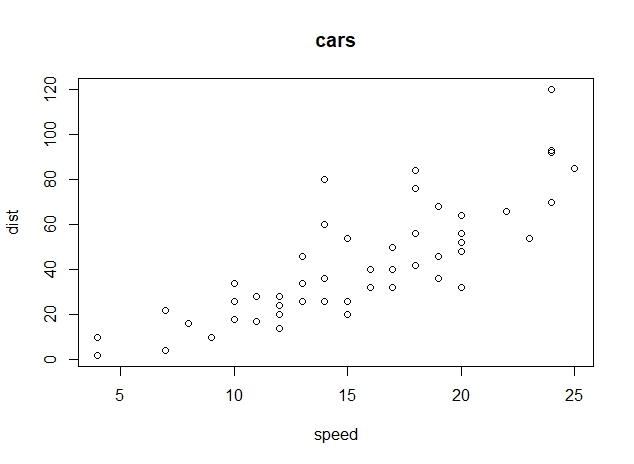
散布図を見ると、正の相関があって、右肩上がりの直線が描けそうです。
- 相関係数を調べる
「speed:速度」と「dist:距離」の相関があるか確認してみます。
> cor(cars$speed, cars$dist) ### 相関係数 [1] 0.8068949
相関係数は約0.8で、正の相関があることがわかりました。
単回帰分析を実行
単回帰分析を実行してみます。
### 単回帰分析を実行 result <- lm(dist ~ speed , data=cars) result
単回帰分析をしたいときは、lm()を使います。

実行した結果は以下の通りです。
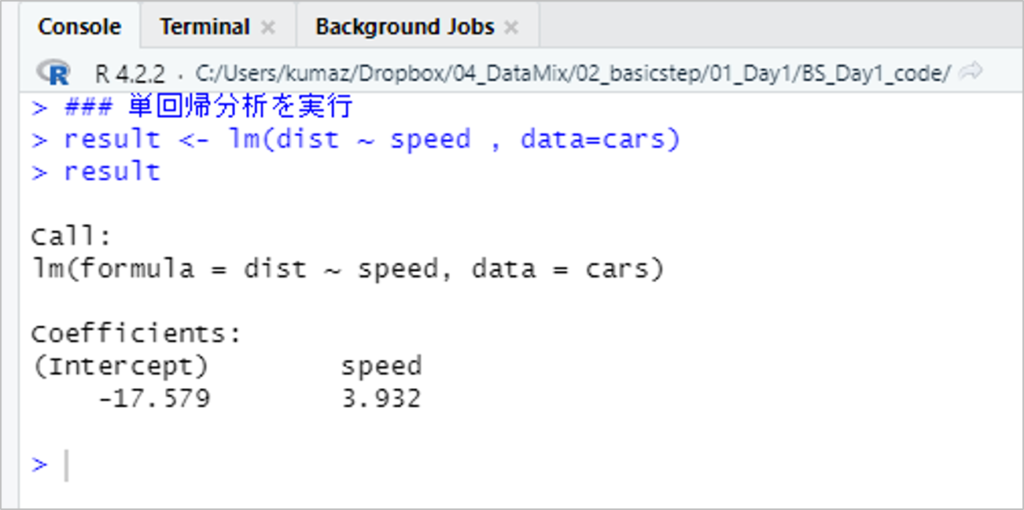
- formula:回帰式
- Coefficients:係数
- Intercept:切片
結果より、「speed:速度」の係数は3.932、切片は-17.579だとわかりました。
つまり…
(dist:距離)= 3.932 ×(speed:速度)- 17.579
単回帰分析の要約統計量
単回帰分析の要約統計量を求めてみます。
### 回帰分析結果の要約統計量 result %>% summary
実行した結果は以下の通りです。
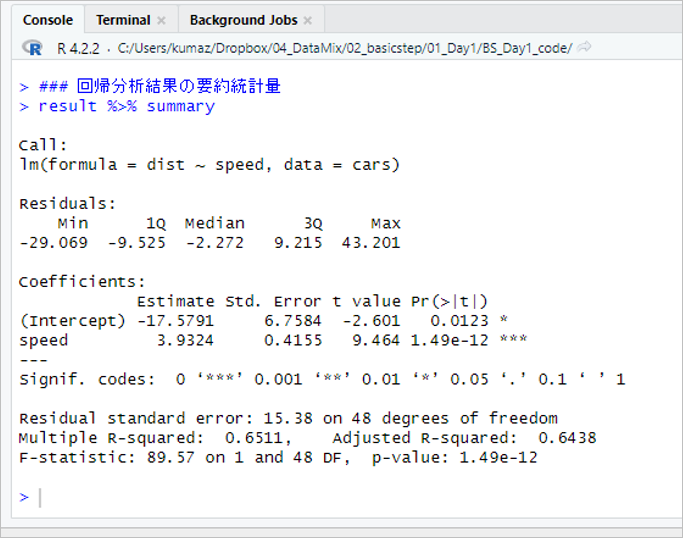
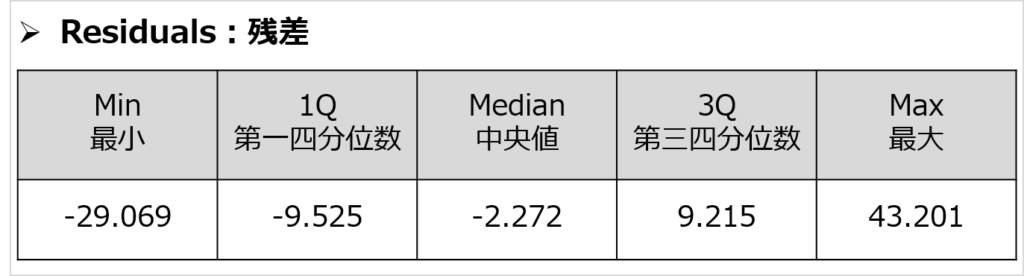
結果の欄は、3つに分けてみることができます。
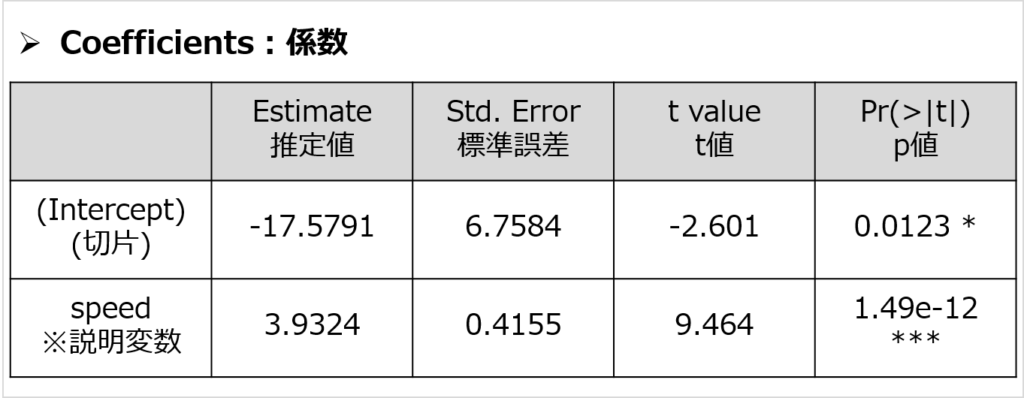

- 回帰式を描画
散布図に回帰式を描画してみます。
plot(cars) abline(result,col="red")
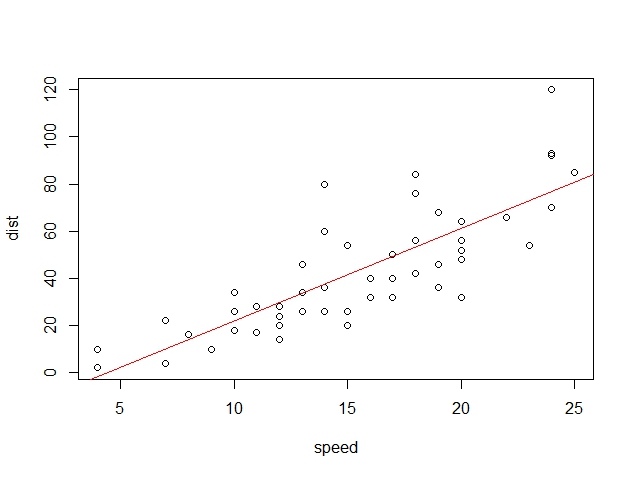
グラフを見ると、直線から外れている値もありますが、おおむねフィットしているとわかります。
回帰の診断
線形回帰の前提条件を満たしているか調べてみます。
##### Diagnostic Plot & Validation 回帰診断 result %>% autoplot(1:4)
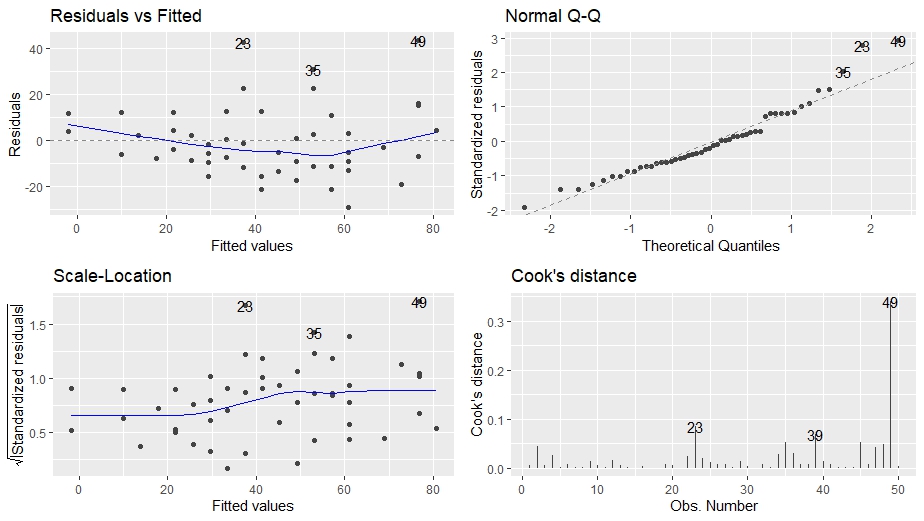
4つのグラフが描画されました。
ひとつひとつ見てみましょう。
- Residual vs Fitted:残差の等分散性のチェック
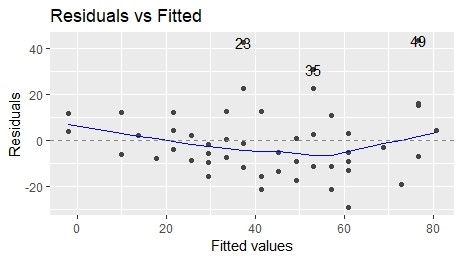
横軸は「目的変数の値」、縦軸は「残差」をプロットしています。
「23, 35, 49」など、一部の残差は値が大きくなっていますが、わりとバラついていて等分散性があるように見えます。
- Scale-Location
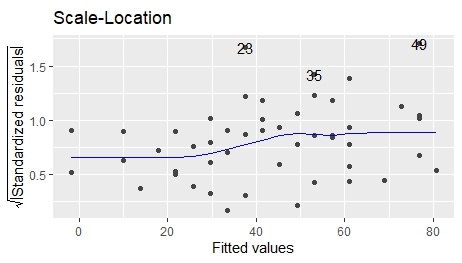
こちらは、ひとつめのResidual vs Fittedの数値を変換した図です。
横軸は「目的変数の値」、縦軸は「基準化した残差の平方根」をプロットしています。
同じように、わりと均一にバラついているようです。
- Normal Q-Q:正規性のチェック
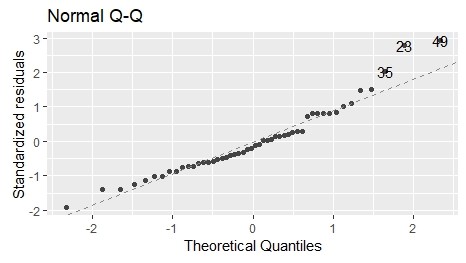
残差が正規分布に従っている場合は、直線上に並びます。
直線状に並んでいなければ、正規分布していません。
図を見ると、「23, 35, 49」のデータは直線から大きく外れていることがわかります。
- Cook’s Distance:クックの距離
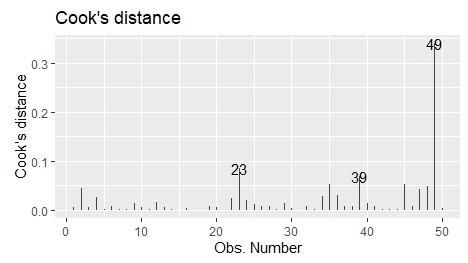
横軸は「個々のデータ」を表していて、それぞれのデータが外れ値になっていないかを判断できます。
1を超えると「かなり外れ値っぽい」、0.5を超えると「怪しい」というのが目安です。
49番目のデータが外れ値のように見えますが、「0.3」くらいなので許容範囲だと考えられます。
- 回帰の診断から見えてくること
線形回帰モデルで結果を出すことはできますが、残差が等分散ではなかったり、正規性に従っていなかったりすることがあります。
その場合、推定された回帰係数や目的変数の推定の精度が低いのではないか、と解釈できます。
また、外れ値があることも見えてくるので、次のアプローチにつなげることが可能です。
回帰診断後のアプローチ例
- 線形モデルではなく、非線形のモデルを使ってみよう
- 説明変数を工夫してから、もう一度モデルに入れてみよう
- 外れ値を処理してから、もう一度モデルに入れてみよう
R言語で重回帰分析

ここからは、Rを使って単回帰分析をやってみます。
実際の講義では、ユニセフのデータを使って進められました。
今回は、Rのデータセットにある「airquality」のデータを使って分析します。
データのセットアップ
はじめに「airquality」のデータを読み込み、どんなデータになっているのか見ていきます。
data(airquality) ### データセットを読み込む head(airquality) ### 見出しを確認 View(airquality) ### 表が出力される airquality %>% glimpse ### 横方向にデータの一覧を見れる
「View(airquality) 」の結果は以下の通りです。
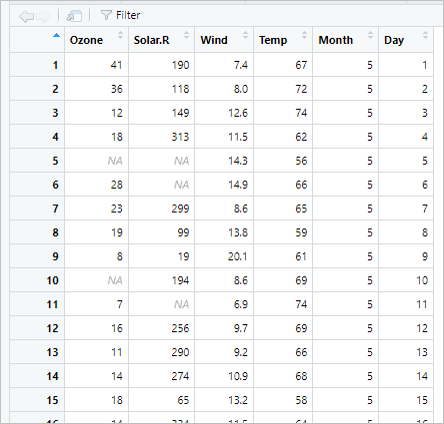
- Ozone:オゾン量
- Solar.R:太陽放射量
- Wind:風力
- Temp:気温
- Month:月
- Day:日
「airquality」のデータは、オゾン量や気温などの気象データです。
6列153行のデータとなっています。
- 要約統計量
「airquality」データの要約統計量を求めてみます。
### airqualityの要約統計量 airquality %>% summary
実行した結果は以下の通りです。
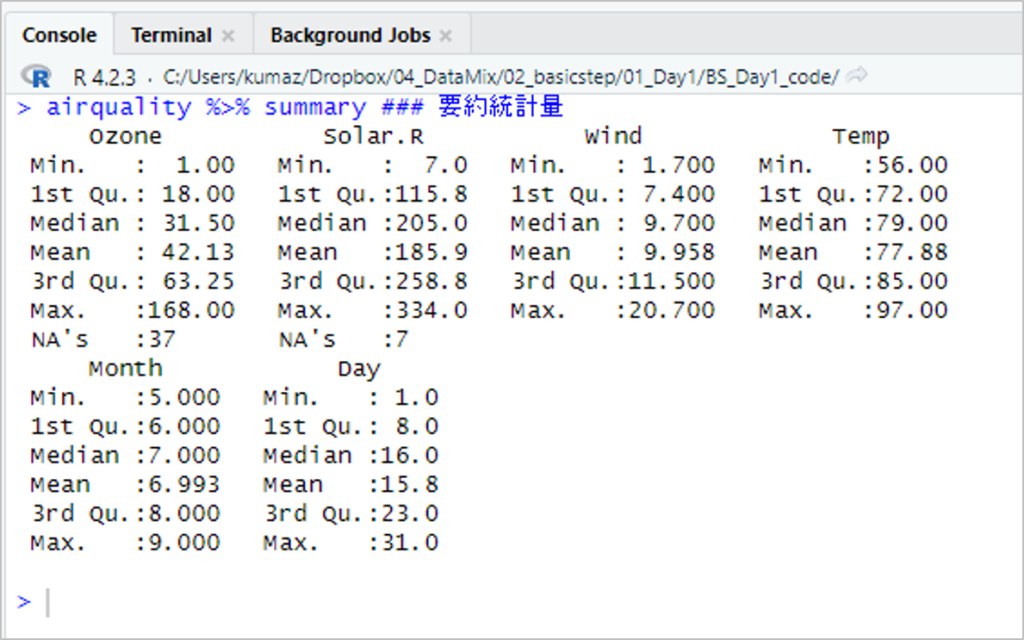
「Ozone」には欠損データ(NA's)が37個、Solar.Rには欠損データが7個ありました。
「Temp」は、摂氏(日本の気温単位)ではなく、華氏(アメリカの気温単位)なので、数字が大きくなっています。
- 箱ひげ図
各データのバラつきを見るために、箱ひげ図を描いてみます。
### 箱ひげ図 boxplot(airquality)
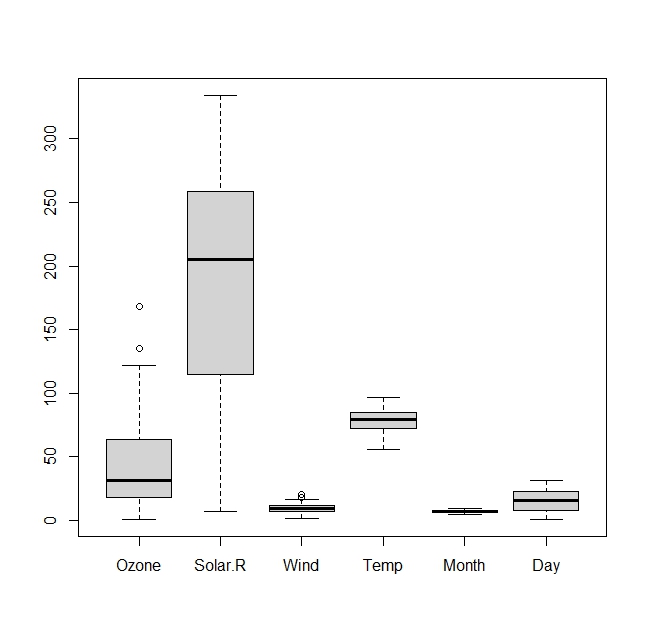
Solar.R(太陽放射量)のデータ範囲が広いです。
重回帰分析を実行
重回帰分析を実行してみます。
### 重回帰分析を実行 air.result <- lm(Ozone ~Solar.R+Wind+Temp, data=airquality) air.result
実行した結果は以下の通りです。

- formula:回帰式
- Coefficients:係数
- Intercept:切片
結果より、「Solar.R:太陽放射量」の係数は0.05982、「Wind:風力」の係数は-3.33359、「Temp:気温」の係数は1.65209、切片は-64.34208だとわかりました。
つまり…
(Ozone:オゾン量)
= (0.05982) ×(Solar.R:太陽放射量)
+ (-3.33359) ×(Wind:風力)
+ (1.65209) ×(Temp:気温)
- 64.34208
重回帰分析の要約統計量
重回帰分析の要約統計量を求めてみます。
### 回帰分析結果の要約統計量 air.result %>% summary
実行した結果は以下の通りです。
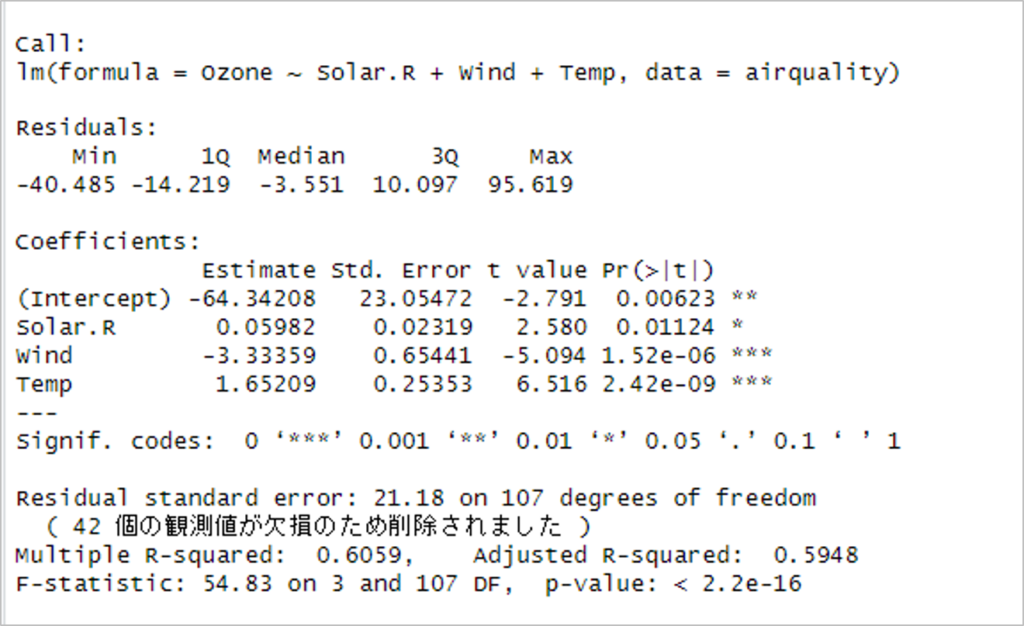
結果の欄は、3つに分けてみることができます。
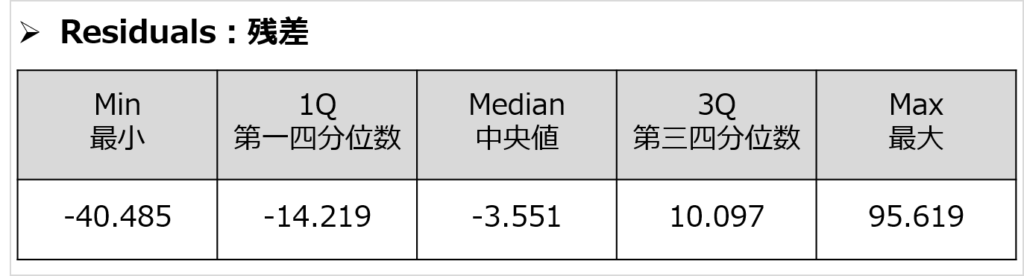
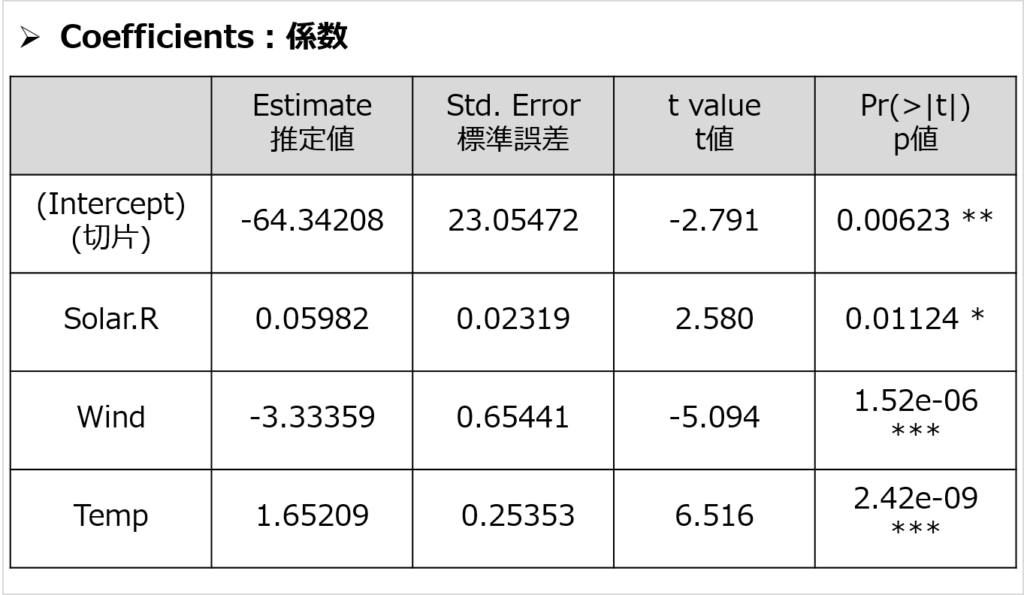

決定係数は0.6059なので、上記の回帰式で6割ほどのデータを説明できたことになります。
回帰の診断
線形回帰の前提条件を満たしているか調べてみます。
##### Diagnostic Plot & Validation 回帰診断#### air.result %>% autoplot(1:4)
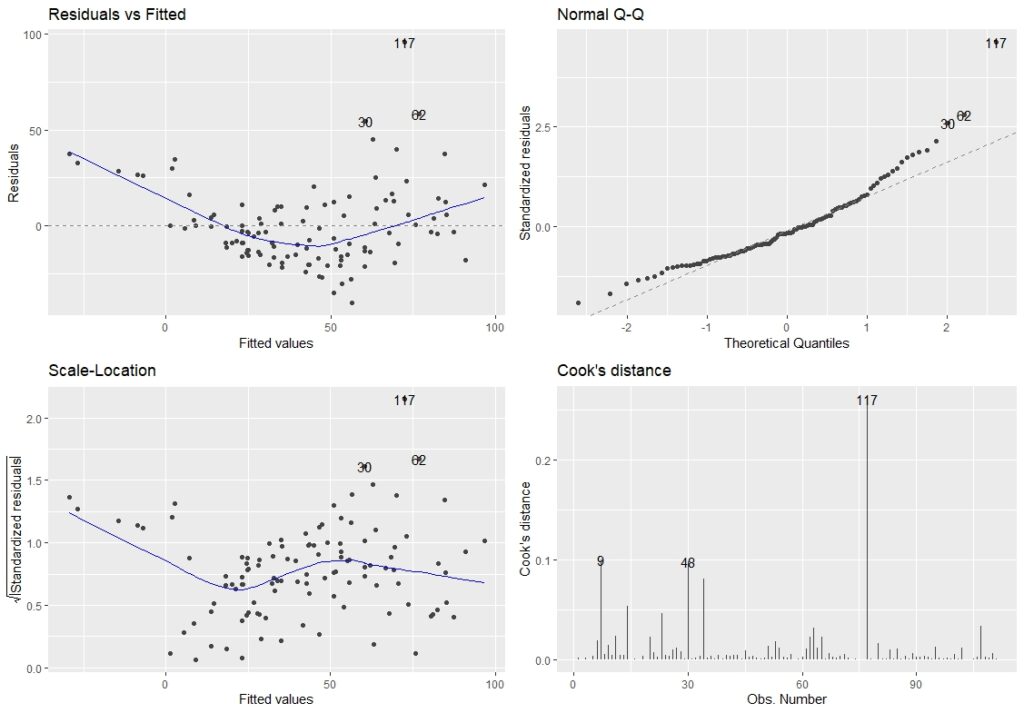
左上の「Residual vs Fitted:残差の等分散性のチェック」を見ると、あまり分散していないように見えます。
右上の「Normal Q-Q:正規性のチェック」も直線上から外れているデータがあり、正規分布していません。
多重共線性の確認
多重共線性に問題があるかどうか確認します。
### 多重共線性の確認 library(car) # carパッケージを使用 print(vif(air.result))

目安として、VIFの結果が10以上だと多重共線性に問題があるようです。
今回は高くても1.4程度なので、多重共線性の問題はなさそうです。
まとめ:線形回帰
今回は、(株)データミックス「気象データアナリスト養成講座」の、講義8日目の内容をまとめました。
講義8日目の内容
- 回帰分析は「lm(目的変数 ~ 説明変数 , data=データセット)」
- 線形回帰の前提条件を満たしているか確認
- 決定係数などの数字からモデルの精度を判断する
- 重回帰分析では多重共線性の確認も必要
今回の講義では、線形回帰の具体的な方法を学びました。
来週の講義もがんばりたいと思います。