
本記事では、(株)データミックスの「気象データアナリスト養成講座」を受けた感想や、講義メモをまとめます。
今回は、2023年3月25日に受けた、ベーシックステップ2日目の内容です。
ロジスティック回帰

講義9日目の内容は「ロジスティック回帰」でした。
講義8日目では「線形回帰」を扱いましたが、比べると以下のような違いがあります。
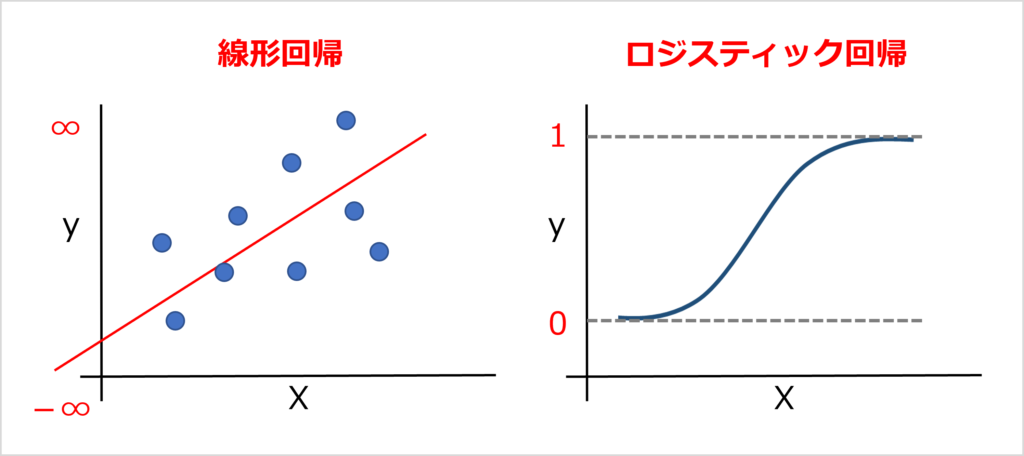
メモ
- 線形回帰は直線で、yは「-∞から∞」の値をとります。
- ロジスティック回帰は「0または1」の二値をとります。
例えば「試験の合格/不合格」や「広告をクリックする/しない」を目的変数とするのがロジスティック回帰です。
ロジスティック回帰の曲線を関数であらわすために、線形回帰の式を変換していきます。
具体的には、「-∞から∞」ではなく「0から1」の範囲におさまるような関数を考えていきます。

ロジスティック回帰の式は上記の通りです。
線形回帰の式をもとにして、「0から1」の範囲におさまるような関数になります。
「0から1」の範囲におさまっているかどうかは、以下の式を考えると確認できます。
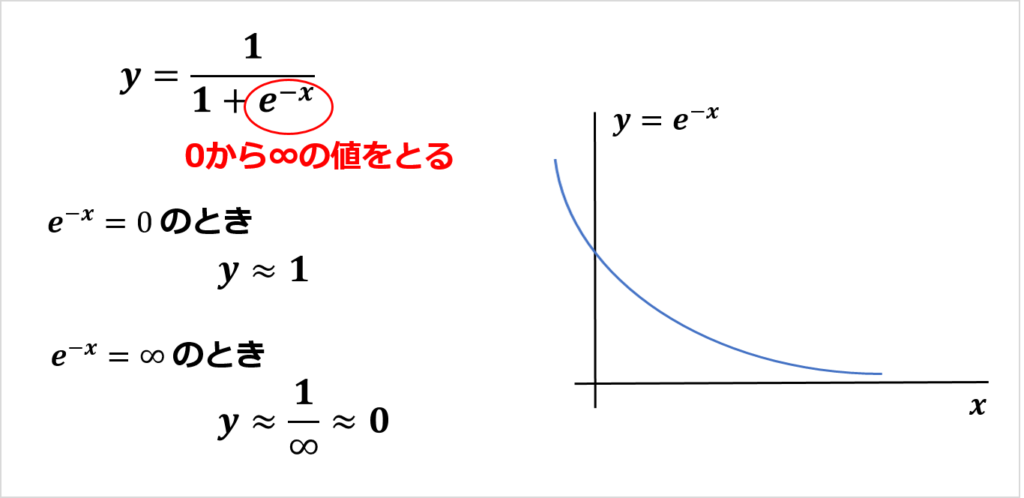
交差エントロピー誤差と最尤推定
線形回帰の「最小二乗法」や「残差の二乗和」と同じように、ロジスティック回帰にも損失関数や計算方法があります。
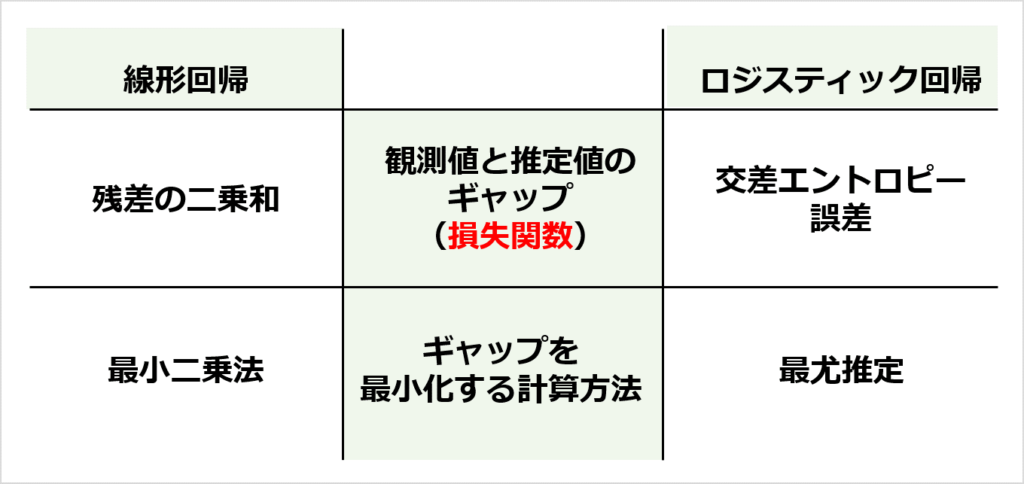
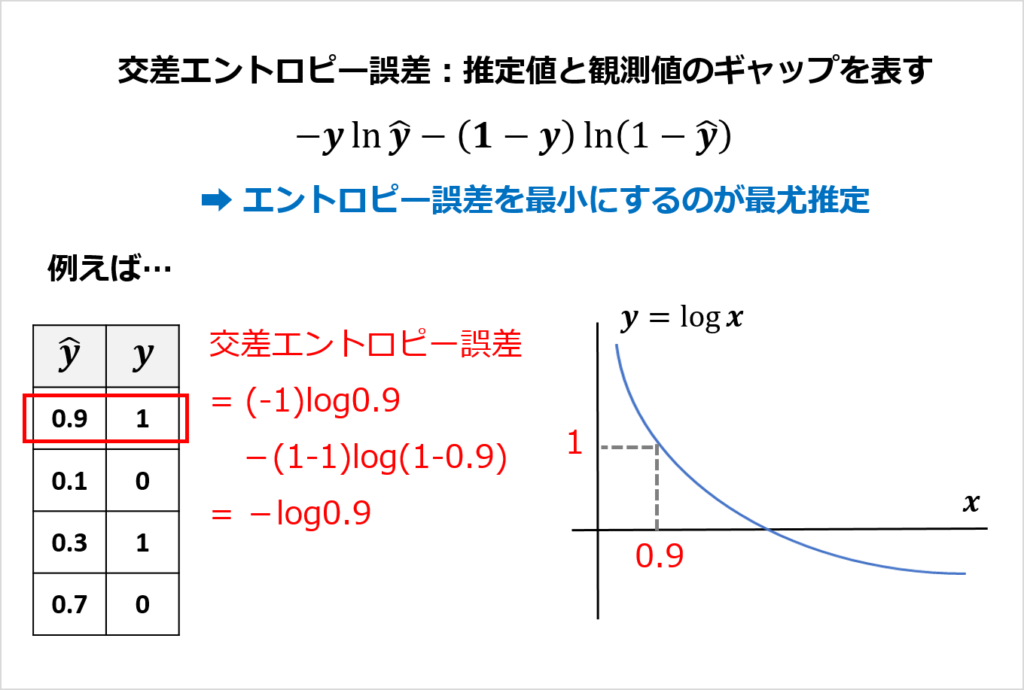
交差エントロピー誤差関数は、たとえば「合格の人には高い推定値を出す/ 不合格の人には低い推定値を出す」を定式化したものです。
交差エントロピー誤差を最小化するようにモデルのパラメータを求める方法が最尤推定です。
オッズ比
「ある事象の起こりやすさ」を表す指標として、オッズがあります。
2つのオッズの比をオッズ比といいます。
例えば、「喫煙の有無」と「肺がんのリスク」に関するデータがあったとき、オッズとオッズ比は以下のようになります。
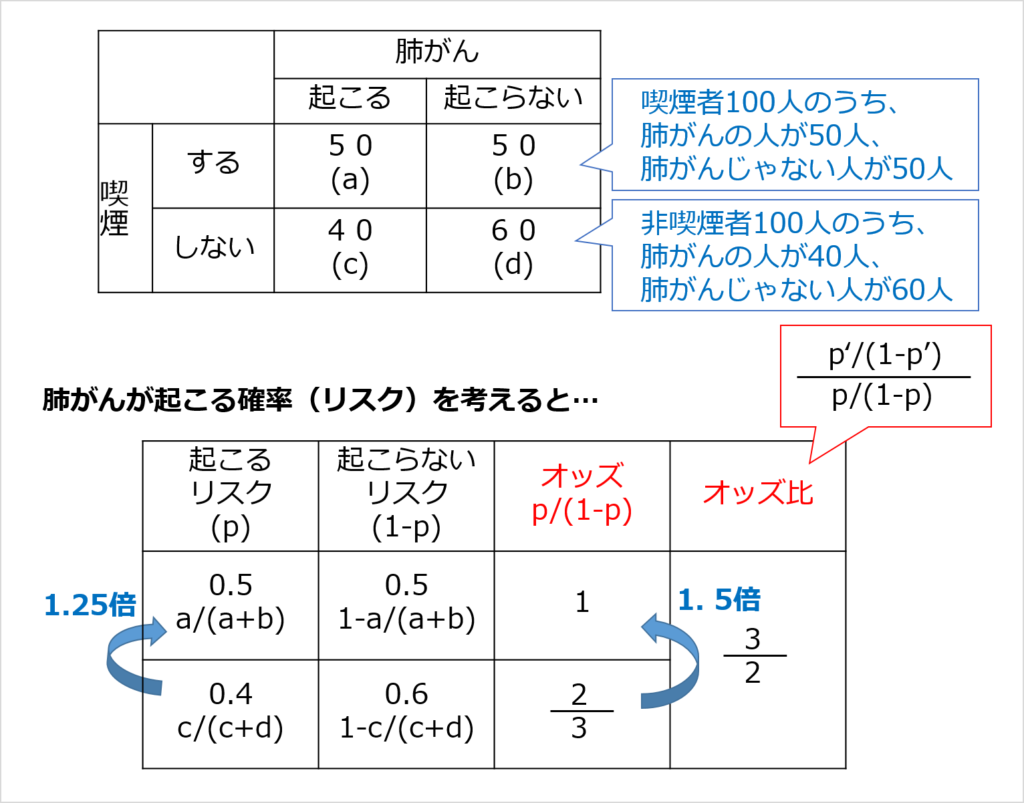
上記のデータでは、リスク比は1.25、オッズ比は1.5になりました。
「(a) << (b)」かつ「(c) << (d)」のとき、オッズ比とリスク比はほぼ等しくなります。
- オッズ比とロジスティック回帰の関係
オッズ比は「eβ」であらわすことができます。
ロジスティック回帰のモデル式を変形して、オッズ比との関係を考えてみます。
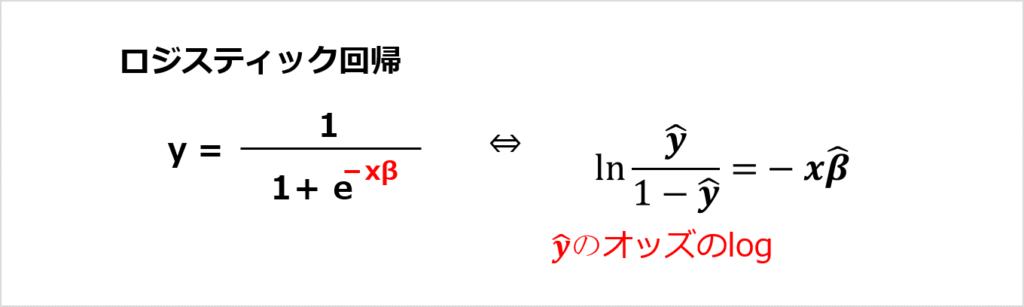
ロジスティック回帰の式を変形していくと、オッズ比として解釈可能になります。
R言語でロジスティック回帰

ここからは、Rを使ってロジスティック回帰分析をやってみます。
実際の講義では、PimaIndiansDiabetes(ピマインディアン女性の糖尿病データ)のデータを使って進められました。
今回は、Rのデータセットにある「birthwt」のデータを使って分析します。
データのセットアップ
はじめに「birthwt」のデータを読み込み、どんなデータになっているのか見ていきます。
「birthwt」は「低出生体重児に関連する危険因子」のデータです。
library(MASS) data(birthwt) ### データセットを読み込む head(birthwt) ### 見出しを確認 View(birthwt) ### 表が出力される birthwt %>% glimpse ### 横方向にデータの一覧を見れる
「View(birthwt) 」の結果は以下の通りです。
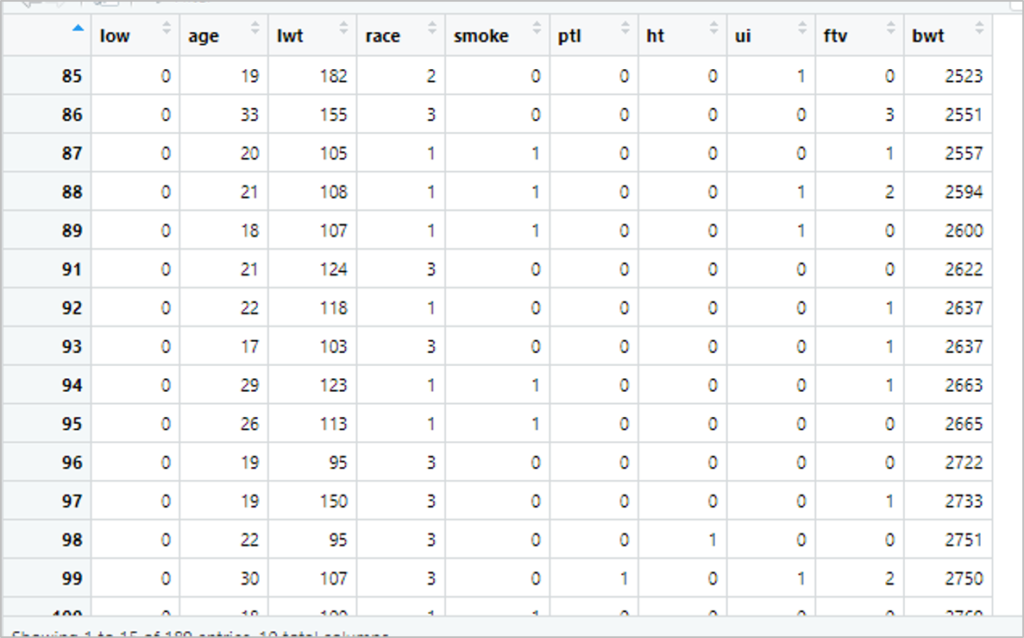
- low:出生時体重が2.5kg未満の指標(2.5kg未満は1)
- age:母親の年齢
- lwt:母親の体重(単位はポンド)
- race:母親の人種(1= 白, 2= 黒, 3= その他)
- smoke:喫煙の有無(喫煙有りが1)
- ptl:早産経験の有無(経験有りが1)
- ht:高血圧の有無(経験有りが1)
- ui:子宮過敏症の有無(有りが1)
- ftv:医師の訪問数
- bwt:出生体重(単位はグラム)
今回、目的変数(y)とするのは「low:出生時体重が2.5kg未満の指標(2.5kg未満は1)」のデータです。
- 出生時体重が2.5kg以上:0
- 出生時体重が2.5kg未満:1
それぞれの説明変数(age~bwt)がどのくらい説明できるのか、ロジスティクス回帰モデルを作ってみます。
EDA(要約統計量)~前処理
まずは「birthwt」の要約統計量などをチェックして、データの前処理をおこないます。
table(birthwt$low) birthwt %>% summary
「low」には、0のデータが130個、1のデータが59個あることがわかりました。
「summary」の結果は以下の通りです。
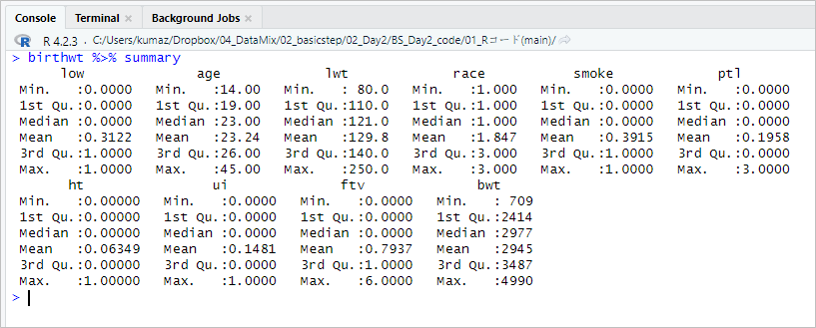
- 欠損値の処理
ロジスティクス回帰では、欠損値(Naデータ)があるとエラーになります。
そのため欠損値があるときは前処理が必要です。
以下のコードで欠損値の処理ができます。
df_na_omit <- na.omit(birthwt) df_na_omit %>% summary
- 外れ値の処理
今回のデータを見てみると、「ptl:早産経験の有無(経験有りが1)」に「2」と「3」のデータがあります。
ptlは「0または1」のデータのはずなので、「2」と「3」のデータは削除します。
## ptlが1より大きいデータを除外する birthwt_sub <- birthwt %>% filter(ptl <= 1)
ロジスティクス回帰
ロジスティクス回帰モデルを作ります。
試しにすべての変数を使ってモデルを作ってみました。
model_logistic <- glm(low ~., data = birthwt_sub, family = binomial)

このロジスティクス回帰モデルを実行すると、以下のエラーになりました。
Warning messages: 1: glm.fit: アルゴリズムは収束しませんでした 2: glm.fit: 数値的に 0 か 1 である確率が生じました
どうやら「bwt:出生体重(単位はグラム)」が含まれていると、エラーになるようです。
なので「bwt」を除いて再度ロジスティクス回帰モデルを作っていきます。
birthwt_result <- birthwt_sub[,c(1,2,3,4,5,6,7,8,9)] model_logistic <- glm(low~., data = birthwt_result, family = binomial) model_logistic %>% summary
結果は以下の通りです。
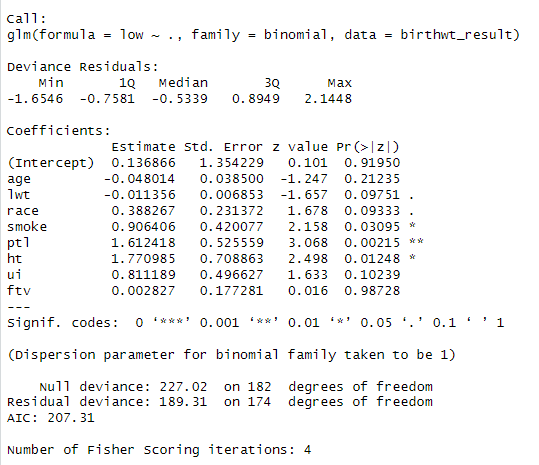
線形回帰モデルと似たような出力結果となりました。
ptl, ht, smokeのp値は、有意水準0.05以下で有意とされます。
予測結果の確率
ロジスティクス回帰モデルは0から1の間の確率で出力されるので、その値を具体的に見てみます。
##予測結果の確率(0-1の間) pred_proba <- predict(model_logistic, type = "response") pred_proba %>% head
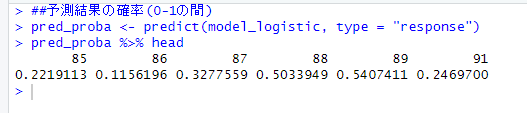
各データに対して、「出生時体重が2.5kg未満:1」となる確率が返ってきました。
「行番号85のデータ:22%」「行番号86のデータ:12%」...であるとわかります。
この結果をグラフ化して見てみます。
## 予測結果(確率)をdata frameに追加
df_pred <- birthwt_sub %>%
mutate(pred_proba = predict(model_logistic, type = "response") )
## low変数を因子型に変換
df_pred$low <- factor(df_pred$low, levels = c(0, 1), labels = c("2.5kg以上", "2.5kg未満"))
## 予測結果のヒストグラム (予測結果の確率 w. 実際の色)
df_pred %>%
ggplot(aes(x=pred_proba, colour=low))+
geom_histogram(aes(y=..density.., fill=low), alpha=.3, position="identity") + geom_density(aes(colour = low), size =1)+
geom_vline(xintercept=0.5, linetype="dashed")
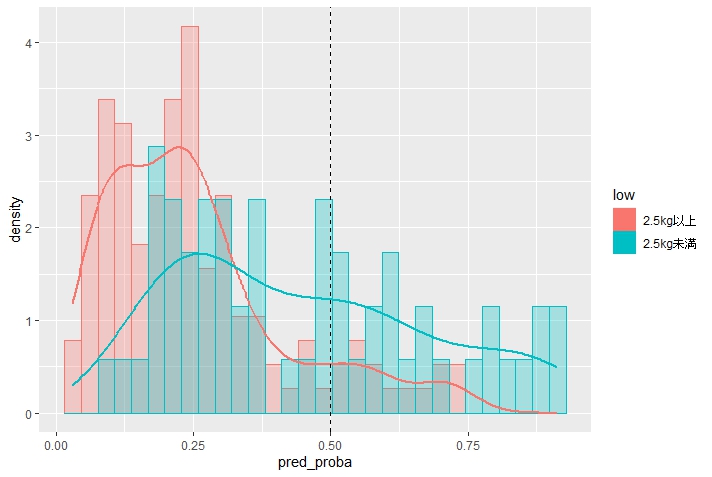
グラフを見ると、赤と青が重なっているところが多くあります。
本当は「左に赤いグラフ、右に青いグラフ」となるのが理想ですが、今回の結果ではハッキリ分かれませんでした。
特に青いグラフが左側にも多くあります。
「出生時体重が2.5kg未満」であるにもかかわらず、予測の確率が50%を切るデータが多いです。
今後、予測モデルの改善や、他に使えるデータがないか探す必要があると思います。
相関と因果

講義の後半は「相関と因果」でした。
- 相関:2つの変数で、一方が変化すれば他方も変化するような関係
- 因果:事象Aを要因として、事象Bの結果が起きること
回帰モデルなど、あらゆるモデルは「バイアスがない理想の環境」を想定してつくられます。
しかし現実では、何らかのバイアスが入り込んでしまいます。
なるべくバイアスを減らして、理想環境に近づけることが必要です。
バイアスの種類
相関や因果に発生するバイアスは、大きく4種類あります。
バイアス
- 偶然
- 反対
- 交絡因⼦(こうらくいんし)
- 選択バイアス
それぞれのバイアスについて見ていきます。
- 偶然
本当は関連性がないのに、偶然にも相関関係が⾒られることがあります。
たとえば「気温が年々上がっている」と「海賊が年々減っている」というのは、グラフにすると相関関係があるように見えてしまいます。
しかし「気温が上がっているから海賊が減っている」わけではありません。
これが偶然のバイアスです。
- 反対
因果の⽅向性が反対になっていることがあります。
たとえば、芸能人がある商品を紹介しているとき、本当は「商品が良いから紹介している」はずなのに、「芸能人か紹介しているから商品が良く見える」ことがあります。
これが反対のバイアスです。
- 交絡因⼦
事象Aと事象Bに因果関係があるように見えて、じつは「別の要因X」が存在していることがあります。
このとき「別の要因X」を交絡因子といいます。
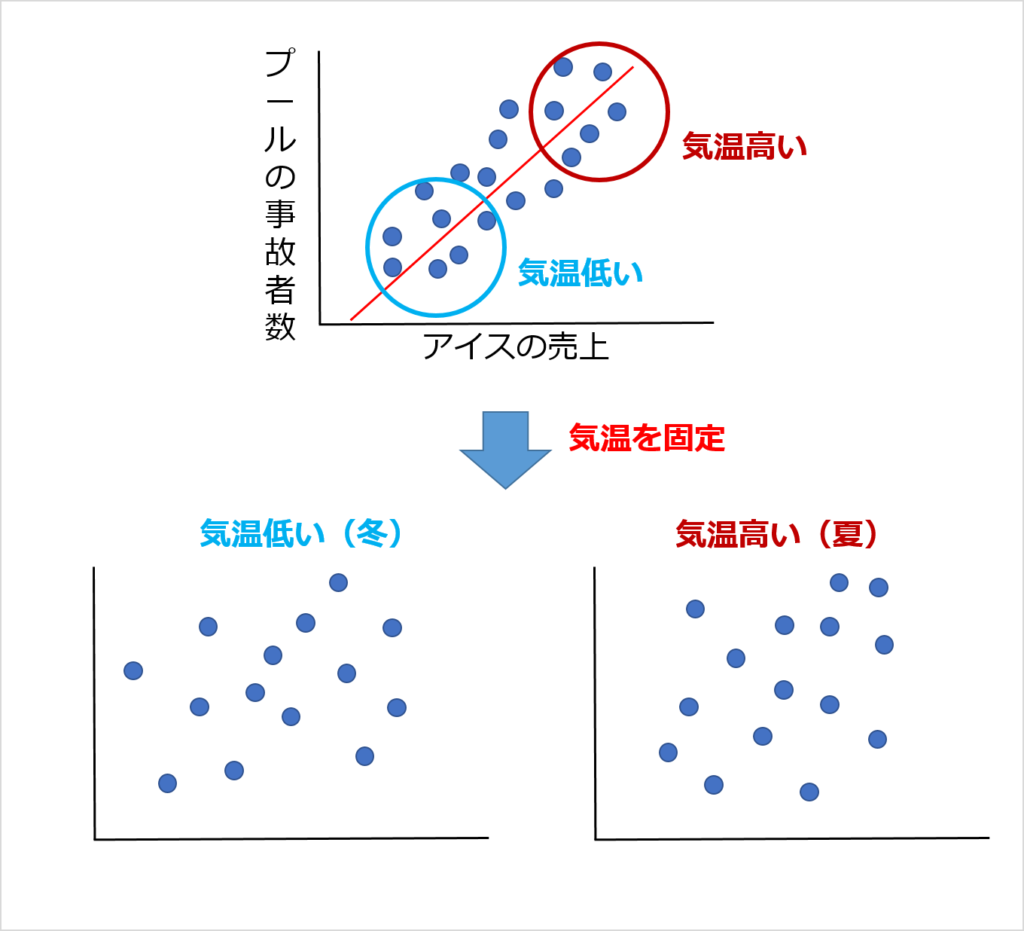
たとえば「アイスの売上」と「プールの事故者数」は、グラフにすると相関があるように見えます。
しかし実際には「気温」という交絡因子があり、「気温」と「アイスの売上」、「気温」と「プールの事故者数」で、それぞれ相関関係があります。
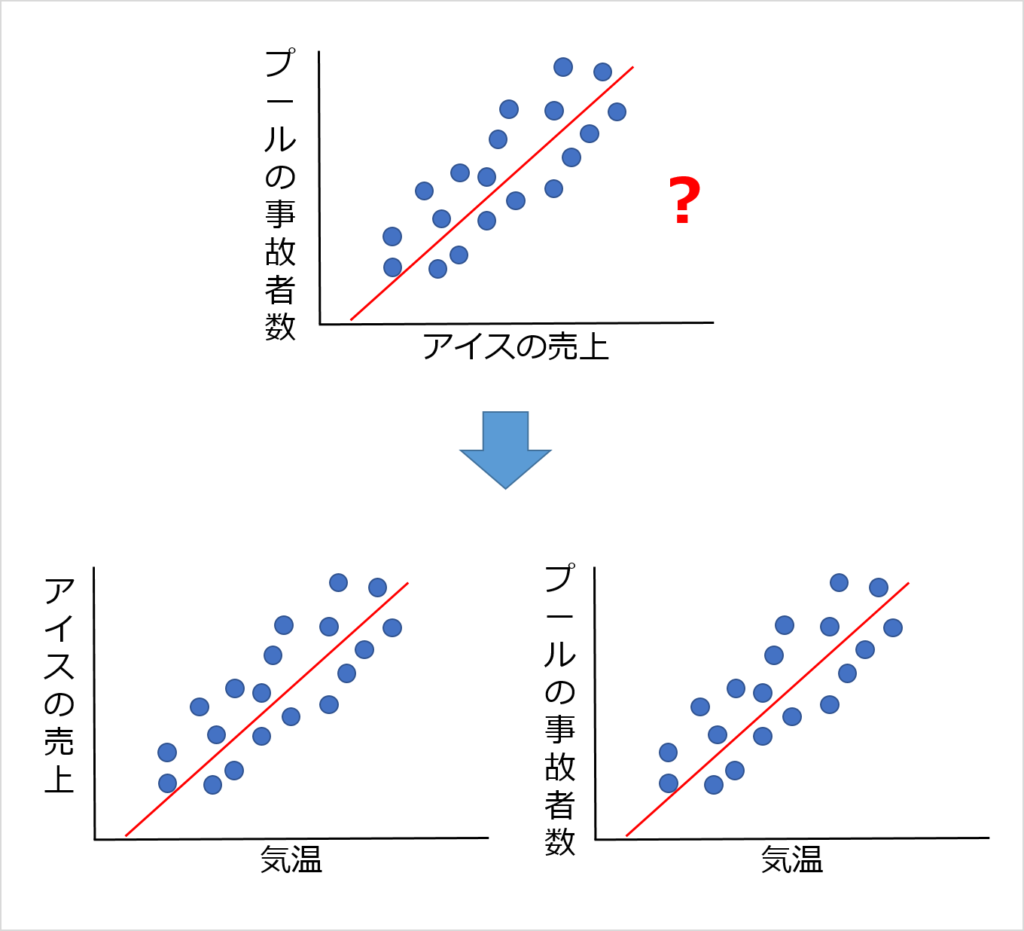
交絡因子によるバイアスがあるときは、交絡因子を固定することで、本来の関係性が見えてきます。
- 選択バイアス
サンプルデータの抽出を誤ってしまうことで、因果関係があるように見えてしまうことがあります。
たとえば、お店の売上を増やしたくてクーポンメールを送った場合を考えます。
- クーポンメール送付する ➡ 売上UP
- クーポンメール送付しない ➡ 売上は変わらず
上記の場合、「クーポンメールのおかげで売上が増えた」と考えてしまいます。
しかし実際には、クーポンメールを送った客は「ヘビーユーザー層」かもしれません。
すると「クーポンメールのおかげで売上が増えた」とは言えなくなります。
このように、⺟集団の代表的なデータを選択できていないのが「選択バイアス」です。
バイアスへの対処
バイアスをなるべく減らすためには、「ドメイン知識(その業界に特化した知見)」と「データ」の両方から判断していく必要があります。
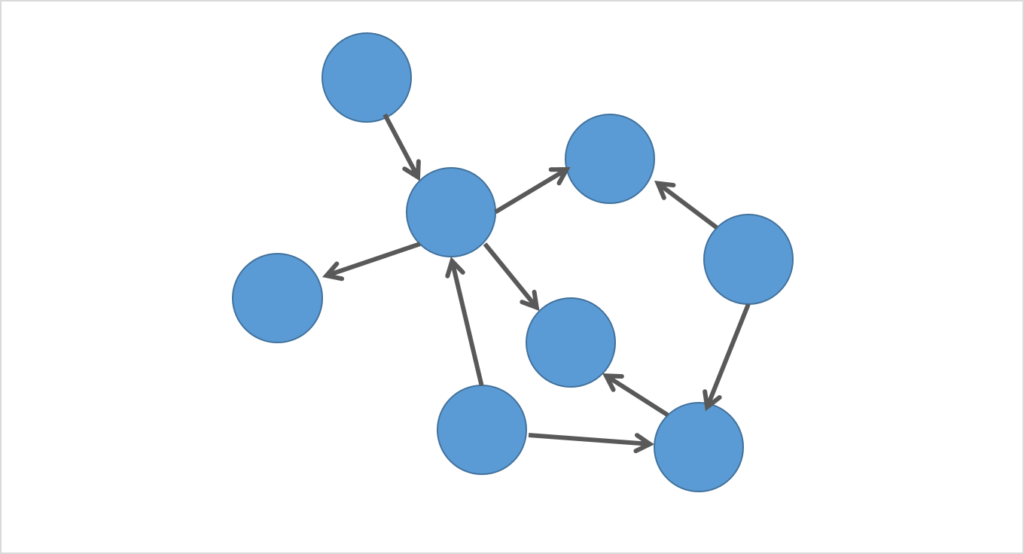
ドメイン知識として仮説を立てるには、ひとつひとつの変数とそれぞれの関係性を描きだすのが有効です。
相関・因果の検証

相関・因果の検証をおこなうためには、A/Bテストなどの実験をおこなう方法と、手元にあるデータから因果関係を探る方法(疑似実験)があります。
それぞれの検証では、妥当性のチェックが必要です。
妥当性
- 内的:疑似相関ではないか?交絡因子はないか?
- 外的:因果関係に⼀般性はあるか?サンプルや検証タイミングを変えても同じになる?
- 統計的結論:統計⼿法に問題はないか?
- 構造:検証した変数や実験の設計、データの計測⽅法は適切か?
実験
因果関係を解釈する方法として、実験があります。
実験するには、コストがかかったり、過去に起きたことだから実験できない状況のときもありますが、可能なら実験したほうが確実なデータが得られます。
たとえば「広告を見せた人と見せなかった人で、売上はどのくらい変わるのか?」という検証を考えましょう。
実験の流れ
- 広告を見せるグループと見せないグループをランダムに抽出
- 広告を見せる/見せない
- 結果の分布を検定していく
ポイントとなるのは、各グループをランダムに抽出することです。
年齢や職業、趣味、家族構成、運動量など、結果に影響を与えそうな要素に偏りがないように抽出します。
そうすると、純粋に広告の効果を測ることができます。
ただし、できるだけ選択バイアスがないようにすると、サンプルが小さくなってしまう可能性があるので、その点は注意が必要です。
疑似実験
データを集めたあとに、擬似的に実験効果を把握するのが「疑似実験」です。
疑似実験には、おもに3つの手法があります。
疑似実験
- 交絡で分割
- モデリング(交絡因子をモデルに入れる)
- 傾向スコア
- 交絡で分割
交絡因子があるのは、「アイスの売上」と「プールの事故者数」の関係のように疑似相関がある場合です。
気温を冬と夏で分けて考えるのと同じように、交絡因子ごとにデータを分割することで各データを比較します。
- モデリング(交絡因子をモデルに入れる)
交絡因子を変数としてモデルに入れることで、疑似実験する方法もあります。
たとえば「広告を見せるグループと見せないグループ」のモデリングであれば、時間帯ごと(0~8時、8時~16時、16時~24時など)に分けて、時間帯を変数としてモデルに組み込みます。
- 傾向スコア
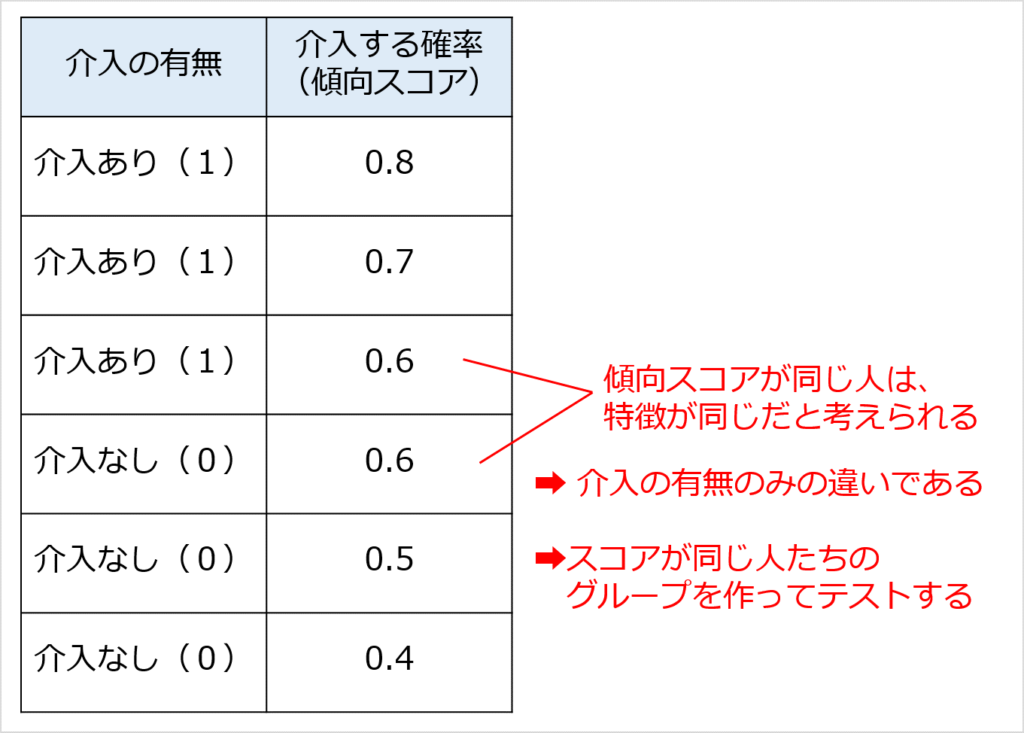
「介入された人達」と「介入されなかった人達」の特徴を使って傾向スコアを予測し、「傾向スコアが同じ人達は似た人たち」とみなして、差分を見ていく方法です。
たとえば…
- 介入された人達:広告を見せたグループ
- 介入されなかった人達:広告を見せなかったグループ
作業としては、「傾向スコアを予測するモデルを作る」ことになります。
予測する対象は「介入する確率」です。
傾向スコアを予測するモデルは、ロジスティック回帰で作ることができます。
傾向スコアは、必要な情報をすべて取れているとき(全交絡因⼦が観測済みの場合)のみ使える手法です。
DAGを描いてみる

DAG(Directed Acyclic Graph)とは、因果関係を可視化してバイアスの特定や処置に活用するツールです。

⽮印と形を使って、因果関係をあらわしていきます。
交絡因子があるときは、交絡因子を加味してモデルに入れます。
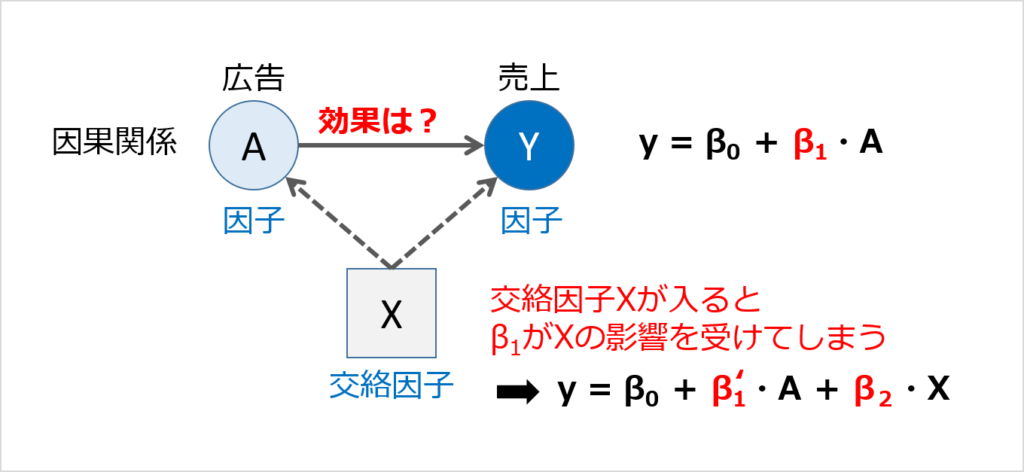
因果関係(A→Y)と外因Xの関係性
ここまで交絡因子について見てきましたが、外因Xには他の因子もあります。
外因X
- 中間因子
- 交絡因子
- 共通因子(合流点)
因果関係(A→Y)に対して、外因Xが影響しているかどうかを考えます。
このとき、バックドア基準という考え方があります。
バックドア基準
- Open:外因Xによる影響が流れ込んでいる
- Close:外因Xによる影響をせきとめられている
現状が「Open/Close」のどちらになっているかを確認し、Closeの状態にしていきます。
- 中間因子
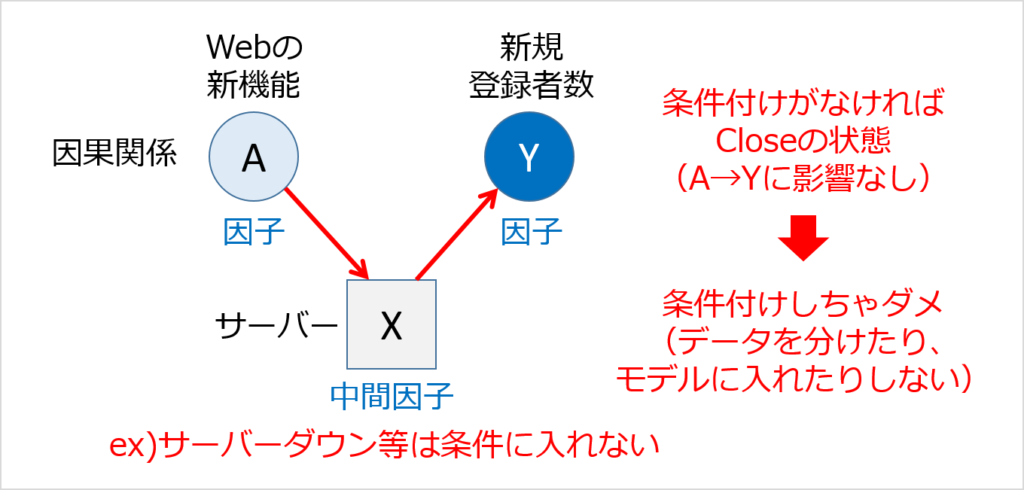
- 交絡因子
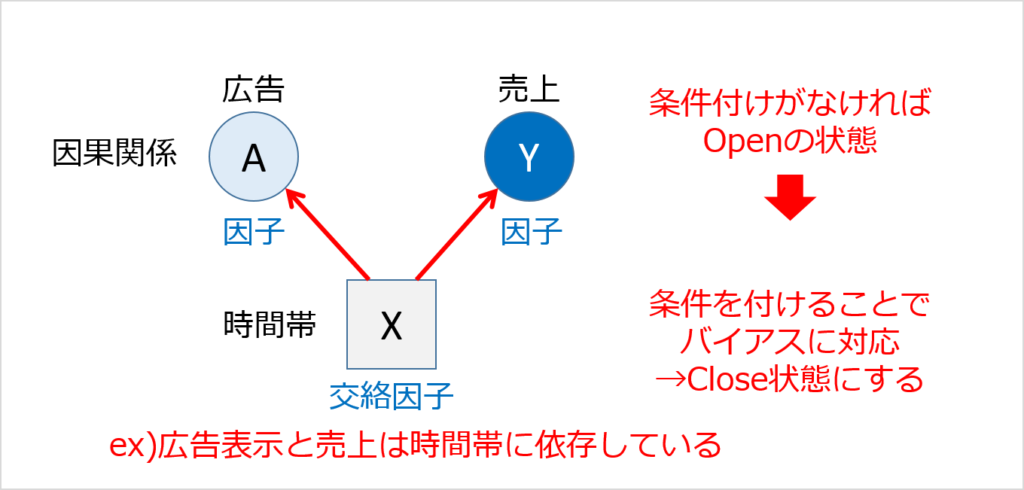
- 共通因子
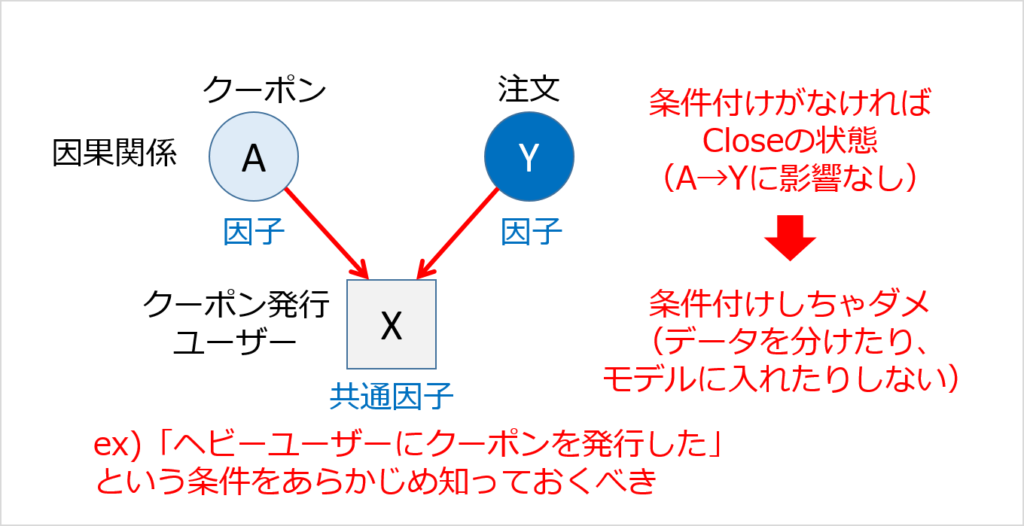
取得できたデータが同じでも、「何を知りたいか」によって、中間因子/交絡因子/共通因子は変わります。
AとYの因果関係を考えるとき、Aは複数ある因子Xのうち”注目した因子”に過ぎないので、人間の関心に合わせて「どの因⼦同⼠が独⽴なのか」を考慮する必要があります。
まとめ:ロジスティック回帰、相関と因果
今回は、(株)データミックス「気象データアナリスト養成講座」の、ベーシックステップ2日目の内容をまとめました。
ベーシックステップ2日目の内容
- ロジスティクス回帰は「glm(目的変数 ~ 説明変数 , data = データセット, family = binomial)」
- 予測結果は確率で出力される
- 相関と因果にはバイアスが存在する
- 相関と因果の検証には実験・疑似実験が使われる
- DAGを用いると因果関係がわかりやすくなる
今回の講義では、ロジスティック回帰の具体的な方法を学びました。
来週の講義もがんばりたいと思います。