
本記事では、(株)データミックスの「気象データアナリスト養成講座」を受けた感想や、講義メモをまとめます。
今回は、2023年3月11日に受けた、ブートキャンプステップ補講の内容です。
回帰分析

講義7日目は、回帰分析の基礎講義でした。
回帰分析とは、「ある変数」と「他の変数」の関係を見るための分析です。
たとえば、「お店の売上」に対して、「メニュー」「価格」「天気」がどんな影響を与えているかを分析できるのが、回帰分析です。
このとき、「お店の売上」は目的変数、「メニュー」「価格」「天気」は説明変数といいます。
目的変数と説明変数の関係を表す式は、回帰方程式(回帰モデル)と呼ばれます。

回帰分析は、「線形回帰」と「非線形回帰」に分けることができます。
さらに線形回帰には、「単回帰分析」と「重回帰分析」があります。
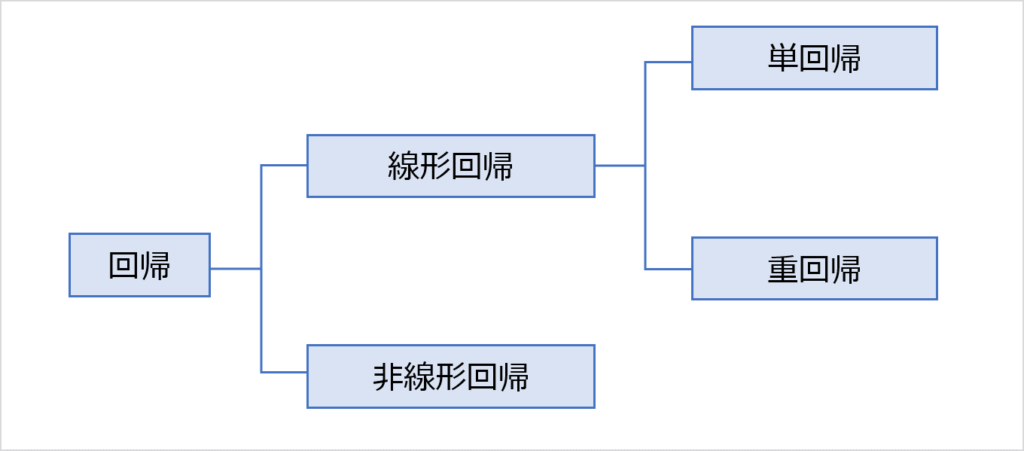
今回の講座では、「単回帰分析」と「重回帰分析」について、詳しい解説がありました。
単回帰分析

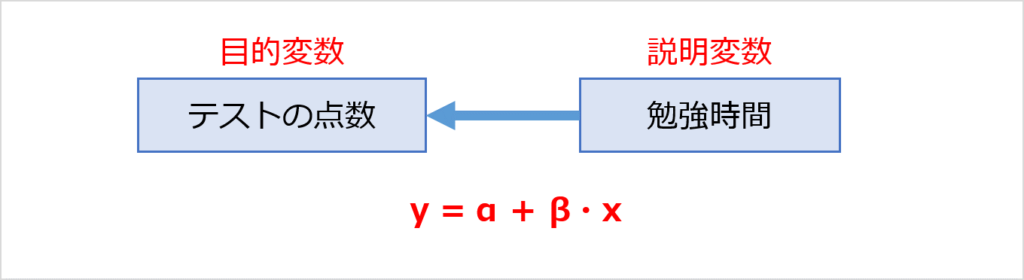
単回帰分析とは、説明変数が1つだけある線形回帰の分析です。
たとえば、「テストの点数」に対して「勉強時間」がどんな影響を与えているかを分析すつのは、単回帰分析になります。
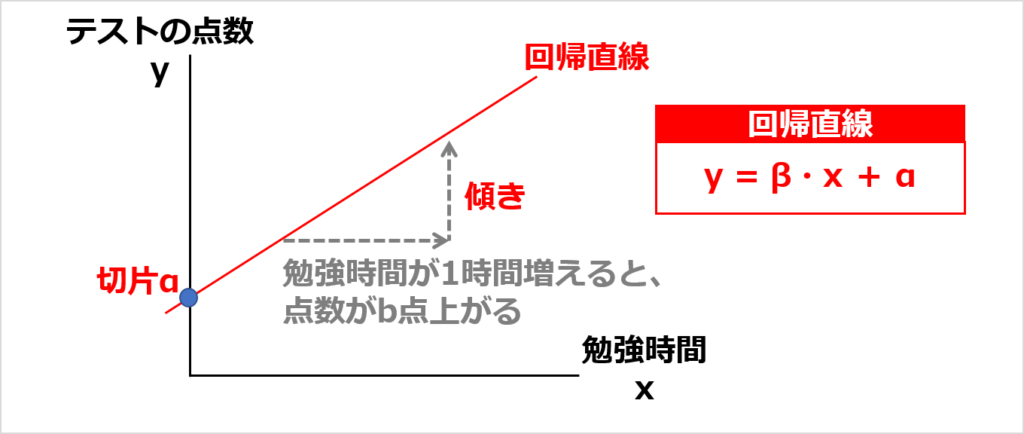
各データの中心的な分布傾向を表す直線を「回帰直線」といいます。
- 回帰直線:y = β・X + α
- y:目的変数
- β:回帰係数
- X:説明変数
- α:切片
回帰直線を求める方法として、最小二乗法があります。
最小二乗法
最小二乗法は、各データの残差の二乗を合計し、その合計が最小となるように回帰直線を選ぶ方法です。
具体的なデータで見ていきます。
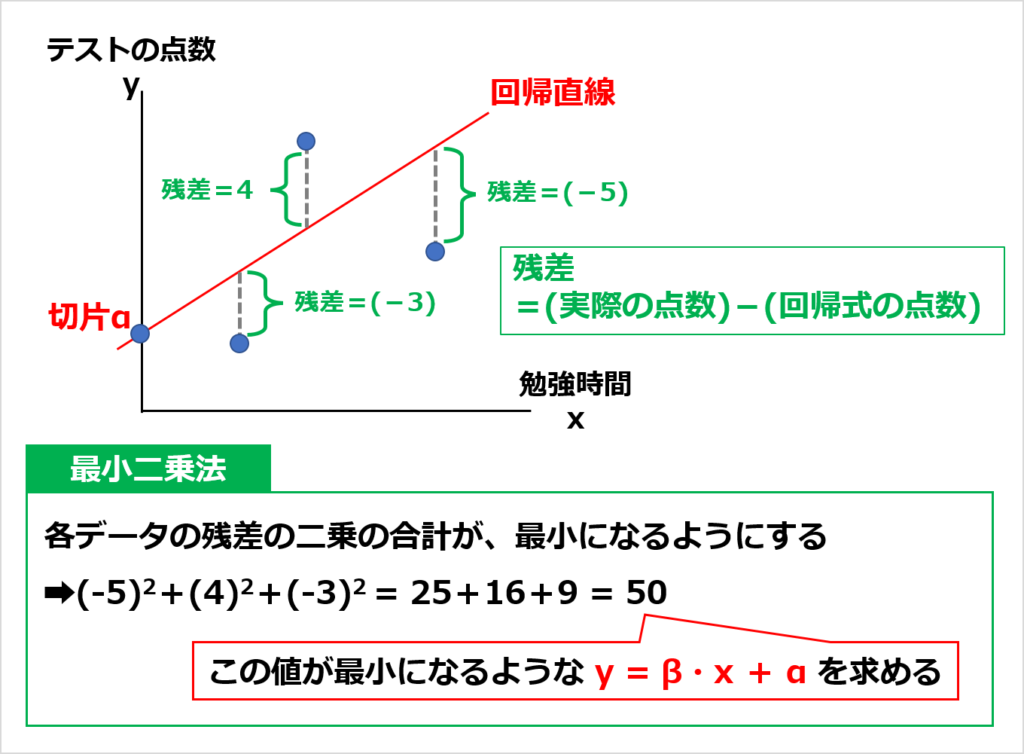
「勉強時間」と「テストの点数」の関係を見たとき、ひとつひとつのデータは回帰直線上にピッタリ乗っているとは限りません。
各データと回帰直線との差を残差といいます。
各データの残差の二乗を合計したとき、その合計値が最小となるように回帰直線を選ぶのが最小二乗法です。
残差と誤差
残差と似た数値として、誤差があります。
この2つは同じように扱われることもあるそうですが、厳密には異なるようです。
- 残差:「サンプルを使って推計した回帰式による値」と「観測された値」の差
- 誤差:「母集団の真の回帰式による値」と「観測された値」の差
残差は、観測されたデータから計算できる値です。
誤差は、「母集団の真の回帰式による値」がわからないため、計算では求められません。
決定係数(寄与率)
決定係数とは、回帰式のモデルの精度をあらわす値です。
平均の線(横線)を100としたときに、回帰直線を引くことで減少した「残差の二乗の合計値」の割合をあらわします。
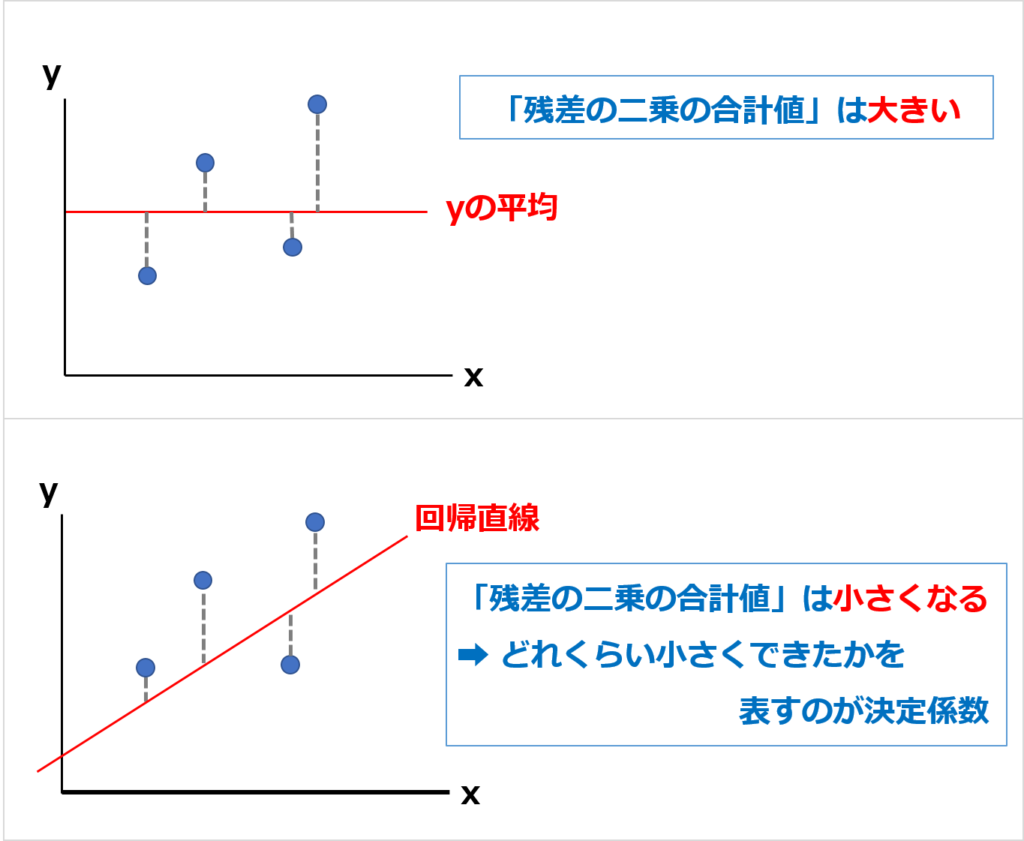
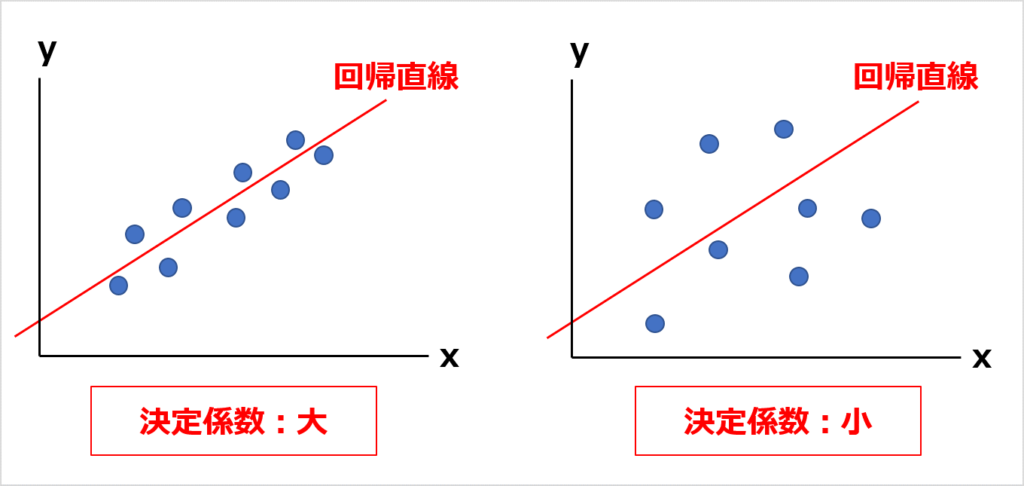
データが回帰直線に近いほど、決定係数は大きいです。
データがバラバラなときは、決定係数が小さいです。
Excelで回帰分析やってみた
回帰直線や決定係数は、Excelで求めることができます。
試しに簡単なデータを作って、Excelで求めてみました。
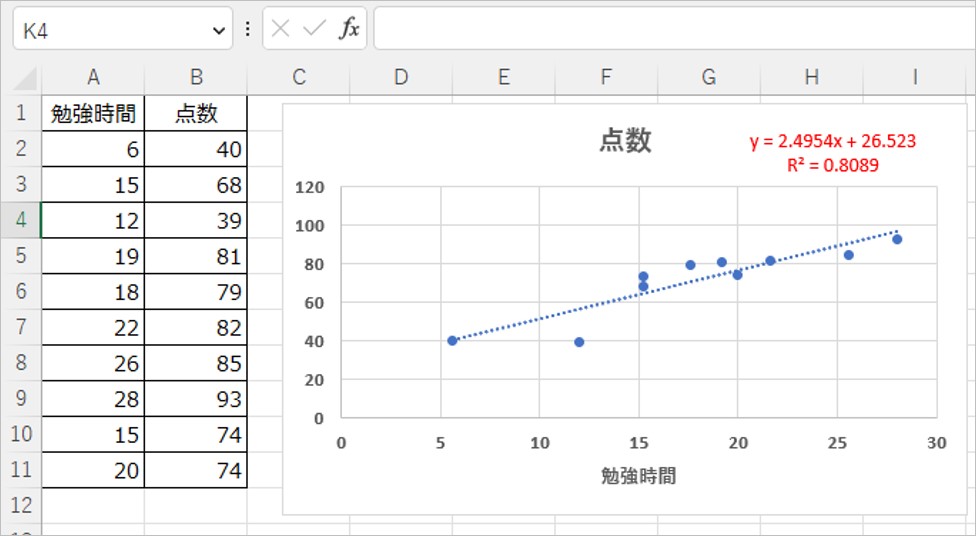
- 回帰直線:y = 2.4954x + 26.523
- 決定係数:R² = 0.8089
決定係数は、通常は0~1.0であらわされます。「1.0 = 100%」です。
重回帰分析

重回帰分析とは、説明変数が複数ある線形回帰の分析です。
- 単回帰分析
- 重回帰分析
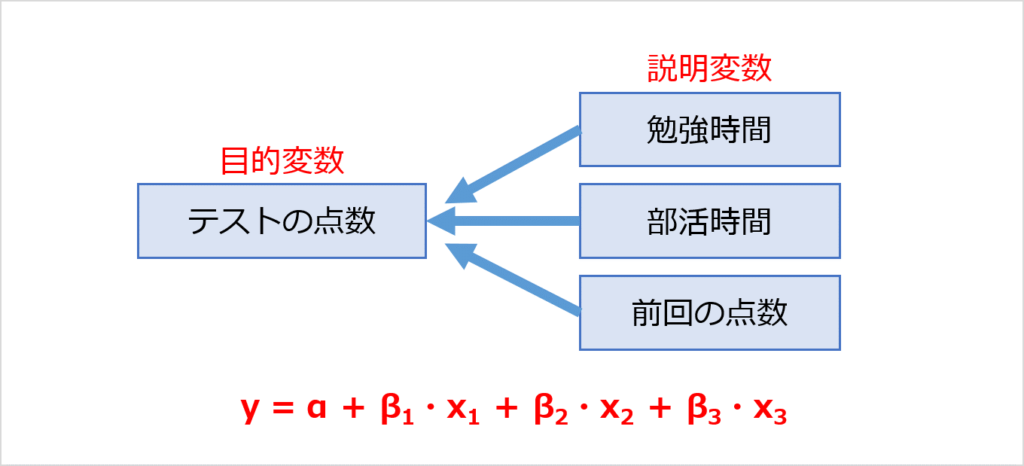
重回帰分析は、(説明変数)×(回帰係数)の項を足し合わせた分析です。
説明変数と決定係数
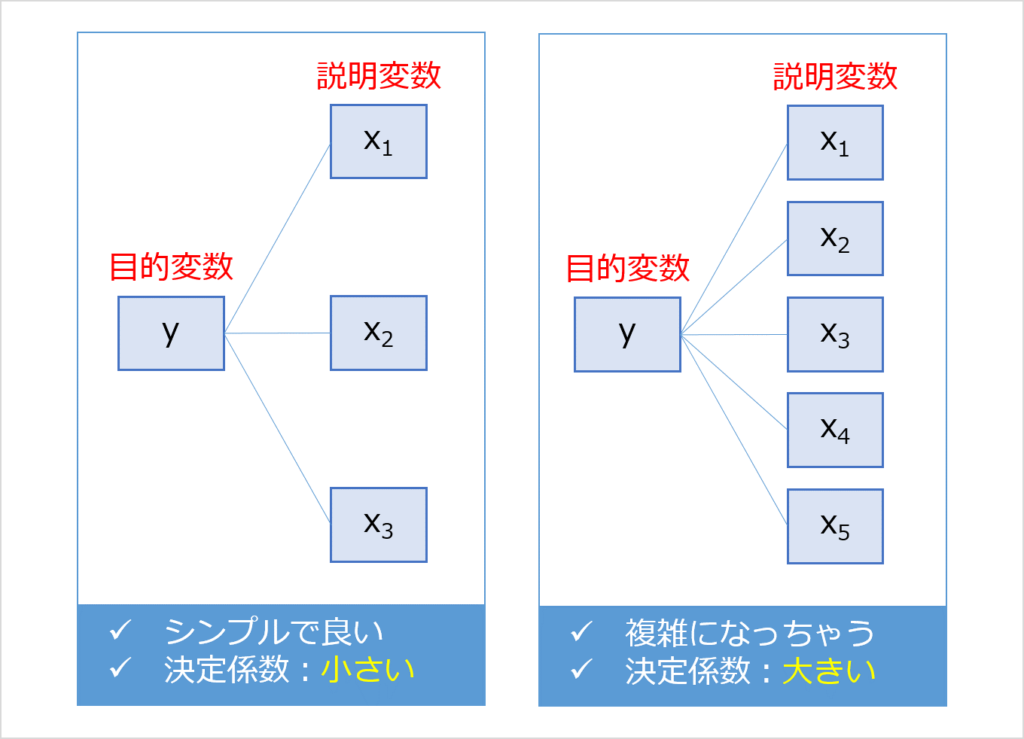
説明変数が3つあるモデルと、説明変数が5つあるモデルを考えます。
両者の決定係数がほぼ同じだった場合、良い分析と言えるのは「説明変数が3つのモデル」です。
しかし一般的には、説明変数が少ないと決定係数は小さくなります。
すなわち、回帰式のモデルの精度は低くなってしまいます。
そのため、説明変数の候補がたくさんあるときは「どれを説明変数に選ぶか」が、とても大切になります。
自由度調整済み決定係数
説明変数の数を増やすと、決定係数は大きくなります。
ほとんど関係のない説明変数であっても、増やせば増やすほど決定係数は大きくなってしまいます。
そのため、決定係数を見て良いモデルを選ぶのは難しいです。

そんなときに使えるのが「自由度調整済み決定係数」です。
自由度調整済み決定係数は、変数の数に応じて決定係数が小さくなるように補正された決定係数のことです。

説明変数の数とのバランスを考えて解釈できる指標が「自由度調整済み決定係数」です。
多重共線性
多重共線性とは、説明変数同士で相関があるせいで、計算が上手くできなくなってしまうことをいいます。

多重共線性の問題を回避するためには、複数の説明変数同士の相関係数を出して、相関係数の絶対値が高い変数の一方を外す必要があります。
まとめ:回帰分析
今回は、(株)データミックス「気象データアナリスト養成講座」の、講義7日目の内容をまとめました。
講義7日目の内容
- 回帰分析は、複数の変数同士の関係を見るための分析手法
- (目的変数)=(回帰係数)×(説明変数)+切片
- 最小二乗法:「残差の二乗の合計値」が最小になるように関係式を求める方法
- 決定係数R2:回帰式のモデルの精度をあらわす
今回の講義は補講という位置づけで、回帰分析の基礎的な内容でした。
来週の講義もがんばりたいと思います。