
本記事では、(株)データミックスの「気象データアナリスト養成講座」を受けた感想や、講義メモをまとめます。
今回は、2023年2月4日に受けた、ブートキャンプステップ2日目の内容です。
講義後半にはRでの演習もありましたが、Rでの演習の内容は以下の記事にまとめています。
講義2日目の内容:統計的・確率的アプローチ

講義2日目の内容は、統計的・確率的な手法の導入でした。
ポイント
確率的では、「1」「0」がハッキリしているわけではない。1から0の間にある割合で考える。
統計的とは、観測不能で未知な"真実"に対して、観測可能な範囲で真実を"推定"すること。
ある課題をデータで解決しようとするとき、すべてのデータを取得するのは難しいです。
たとえば「マクドナルドの客単価」を正確に調べようと思ったら、世界中のすべての店舗の来客数や購入額を調査しなければいけません。
全調査は⾮現実的なので、統計的に"推定"することで、課題を解決していきます。
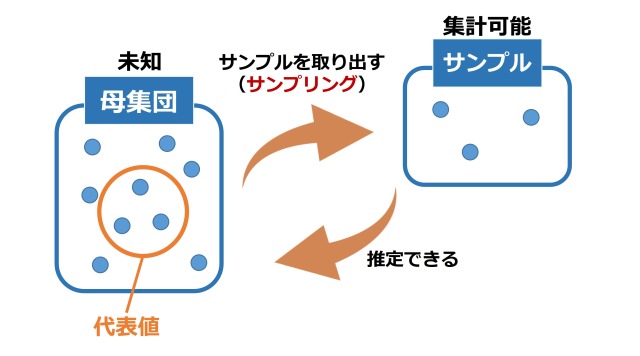
母集団とサンプル
全データを得ることは難しいので、全データのなかから代表的なデータをいくつか取ってきて、全データの傾向を推定していきます。
メモ
- 全データは「母集団」という。
- 代表的なデータは「サンプル」「標本」という。
「母集団」から「サンプル」を取得することを、サンプリングといいます。
サンプリング手法
サンプルを使って推定するときは、「母集団の"本当に知りたいこと"」を知れるかどうか、つねに気にする必要があります。
そのため、目的に応じてサンプリング手法を変えなければいけません。
サンプリング手法は、おもに5つあります。
代表的なサンプリング手法
- 単純無作為抽出
- 層化抽出
- クラスター抽出
- 多段抽出
- 系統抽出
それぞれ、詳しくみていきます。
- 単純無作為抽出
単純無作為抽出は、母集団からランダムに抽出する方法です。
たとえば、100万あるデータから1%(=1万)のデータを適当に取ってくるのは、単純無作為抽出になります。
メリット
- シンプルでわかりやすい
- 先入観なくサンプリングできる
デメリット
- 母集団のリスト作りが大変
- 不均衡なデータが反映できない
- 本当にランダムかわからない場合もある
単純無作為抽出のデメリットとして、不均衡なデータが反映できないがあります。
たとえば、全国チェーン店の来客者からサンプリングすることを考えます。
もし九州の店舗数が少なければ、サンプリングしたときに九州のお客さんのデータ数が0になるかもしれません。
このように、"九州の店舗数が少ない"といった「不均衡なデータ」があると、単純無作為抽出が上手くいかない場合があります。
また、本当にランダムかわからない場合もあるというデメリットもあります。
たとえば、商品の購入者にアンケートを配って回答を得ることを考えます。
そもそもアンケートに回答してくれる人は、「商品のファン」あるいは「クレーマー」の可能性があります。
商品に対して特別な感情がない人の意見は、わかりません。
- 層化抽出
層化抽出は、母集団をグループにわけてから、グループ内でランダムにサンプルする方法です。
たとえば、デパートの利用者を「ブラックカード」「ゴールドカード」「その他のカード」を持つ人でわけてから、購入データを適当に取ってくるのは、層化抽出になります。
メリット
- 不均衡なデータがあっても、取りこぼしがない
- ⺟集団の推定精度が上がる
デメリット
- ⺟集団の構成⽐を、ちゃんと把握していないとNG
- クラスター抽出
クラスター抽出は、母集団をグループにわけてから、グループごとサンプルする方法です。
グループ内のデータは、すべて調査対象となります。
たとえば、全国展開のチェーン店で「新宿店」「難波店」「博多店」のデータを取ってくるのは、クラスター抽出になります。
メリット
- リストの作成がカンタン
デメリット
- 偏りが大きいかもしれない
- 多段抽出
多段抽出は、クラスター抽出を、段階的におこなっていく方法です。
たとえば、東京23区のなかから「港区」を抽出して、さらに港区から「六本木」を抽出して、六本木に住む人からランダムにサンプリングするのは、多段抽出になります。
メリット
- サンプリングの効率が良い→コストを抑えられる
デメリット
- サンプルが⼩さくなると、偏りが大きい
- 系統抽出
系統抽出は、母集団のデータに通し番号を振り、ある番号から一定の間隔で抽出する方法です。
たとえば、来客者に通し番号がついたポイントカードを渡して、10番目の人から5つ飛ばし(10,15,20...)で抽出するのは、系統抽出になります。
メリット
- 単純無作為法より、時間とコストが抑えられる
デメリット
- 通し番号の並び順に何かの規則があると、偏ってしまう
系統抽出のデメリットとして、通し番号の並び順に何かの規則があると、偏ってしまうがあります。
たとえば、10の倍数の顧客には特典を付けている、という前提があると、サンプルデータに偏りが生じてしまいます。
EDAと統計量

EDA(Explanatory Data Analysis)とは、探索的データ解析のこと。
データの特徴を探したり、どんなデータ構造になっているか確認したりする作業を指すようです。
EDAを進めるにあたり、要約統計量の知識が必要になります。
メモ
要約統計量とは、データの特徴や分布状態を表す数値。
要約統計量には、最小値・最大値・平均値・中央値・標準偏差などがあります。
講義では、中央値と標準偏差について、詳しく解説されました。
中央値
データを小さい順に並べたとき、ちょうど真ん中にあたるデータが中央値です。
データの個数が奇数のときは、ちょうど真ん中の1つが中央値になります。
データの個数が偶数のときは、真ん中の前後2つの平均値が中央値になります。

分位数
データを小さい順に並べたとき、2等分したものを二分位数(=中央値)、4等分したものを四分位数といいます。

分位数をパーセントであらわしたものを、パーセンタイルといいます。
ポイント
- 25パーセンタイル(25%)= 第1四分位数(Q1)
- 50パーセンタイル(50%)= 第2四分位数 = 中央値
- 75パーセンタイル(75%)= 第3四分位数(Q3)
75パーセンタイルから25パーセンタイルを引いた値を、四分位範囲(IQR / Interquartile range)といいます。
IQRが大きければ大きいほど、データの散らばり具合は大きくなります。
箱ひげ図
パーセンタイルを可視化した図として、箱ひげ図があります。
箱ひげ図は、分布の大まかな傾向を把握したいときに役立ちます。
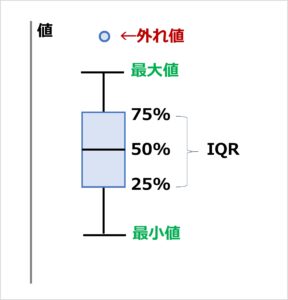
ポイント
- 最大値:「Q3 + 1.5 × IQR」の範囲の最大値
- 最小値:「Q1 - 1.5 × IQR」の範囲の最小値
スケーリング
スケールのちがう2つのデータを比べたいとき、一定のルールに基づいてデータを変換処理することをスケーリングといいます。
たとえば、「100点満点の数学テスト」と「200点満点の英語テスト」の偏差値を出したいとき、スケーリングをおこないます。
おもなスケーリング方法
- 標準化
- 正規化
分散と標準偏差
分散は、データのバラつきをあらわす指標です。
たとえば、テストの点数の分散を考えてみます。
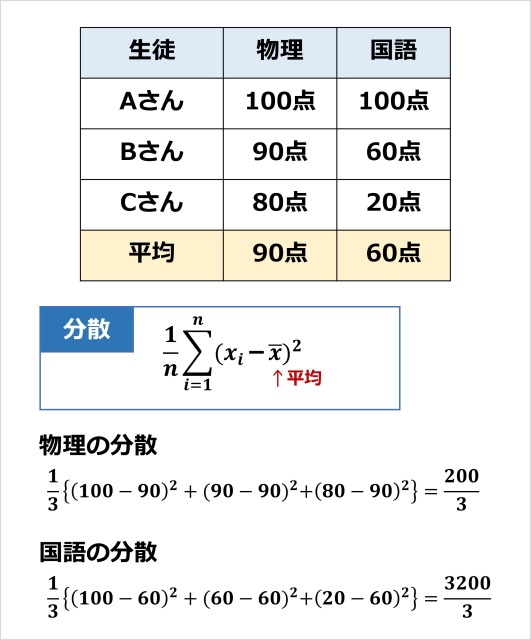
上記の例では、物理の分散よりも、国語の分散のほうが大きいです。
よって国語のほうが、バラつきが大きいことがわかります。
標準偏差は、分散の平方根を取った値です。
不偏分散
実際に分散を求めるときは、ふつうの分散(標本分散)ではなく、不偏分散を使います。
不偏分散は、標本分散の式で「1/n」を「1/(n-1)」に変えたものです。
ポイント
- 標本分散:標本(サンプル)の分散
- 母分散:母集団の分散
- 不偏分散:標本から母集団の分散を推定した分散
- 標本分散は、母分散よりも小さくなる
- 不偏分散を使うことで、母集団をなるべく正確に推定する
共分散
2つのデータの分散をかけあわせたものを、共分散といいます。
たとえば、テストの点数の分散を考えてみます。
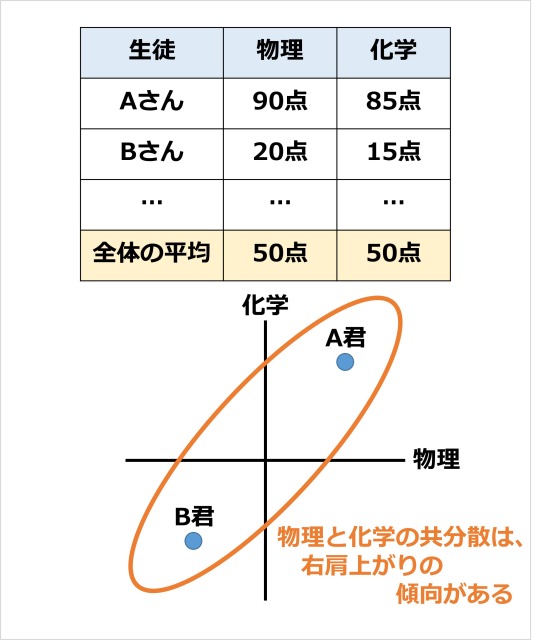
上記の例では、Aさんは理科が得意、Bさんは理科が苦手、というような状況をイメージしています。
他の生徒も、同じような傾向があるはずです。
よって、物理と化学の共分散では、右肩上がりの傾向があると考えられます。
ポイント
共分散では、以下のように解釈できるとOK。
- 右肩上がりの傾向がある → 正の直線関係がある
- 右肩下がりの傾向がある → 負の直線関係がある
- データが散布している → 2つのデータは無関係
共分散では、正負の関係を把握することができます。
しかし、関係の強さを把握することはできません。
関係の強さを把握したいときは、相関係数を使います。
相関係数は、共分散をそれぞれの標準偏差で割ってスケーリングしたものです。
EDAの可視化
EDA(探索的データ解析)でグラフを作っていくにあたり、変数の種類を把握しておく必要があります。
変数が「離散変数(カテゴリ値)」か「連続変数(連続値)」かによって、要約方法が変わります。
- 離散変数(カテゴリ値)

離散変数の基本的な要約方法は、「カウント」や「割合の算出」です。
男女別の人数をカウントしたり、満足度の高い人が何%いるか算出したりします。
- 連続変数(連続値)

連続変数の基本的な要約方法は、要約統計量です。
平均値や中央値、最大値、最小値、標準偏差などを求めます。
まとめ:統計的・確率的アプローチを理解する
今回は、(株)データミックス「気象データアナリスト養成講座」の、講義2日目の内容をまとめました。
講義2日目の内容
- 母集団・サンプル・サンプリング手法を知る
- 要約統計量を理解する
- EDA(探索的データ解析)の可視化
データ分析を進めるうえで必要な、データの確認方法や確率的な考え方を学びました。
講義後半のR演習は、以下の記事をご参照ください。
